题目内容
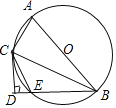
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BCCF=2HE.其中正确的结论有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BCCF=2HE.其中正确的结论有( )
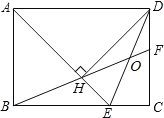
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①根据角平分线的定义可得∠BAE=∠DAE=45°,然后利用求出△ABE是等腰直角三角形,根据等腰直角三角形的性质可得AE=![]() AB,从而得到AE=AD,然后利用“角角边”证明△ABE和△AHD全等,根据全等三角形对应边相等可得BE=DH,再根据等腰三角形两底角相等求出∠ADE=∠AED=67.5°,根据平角等于180°求出∠CED=67.5°,从而判断出①正确;
AB,从而得到AE=AD,然后利用“角角边”证明△ABE和△AHD全等,根据全等三角形对应边相等可得BE=DH,再根据等腰三角形两底角相等求出∠ADE=∠AED=67.5°,根据平角等于180°求出∠CED=67.5°,从而判断出①正确;
②求出∠AHB=67.5°,∠DHO=∠ODH=22.5°,然后根据等角对等边可得OE=OD=OH,判断出②正确;
③求出∠EBH=∠OHD=22.5°,∠AEB=∠HDF=45°,然后利用“角边角”证明△BEH和△HDF全等,根据全等三角形对应边相等可得BH=HF,判断出③正确;
④根据全等三角形对应边相等可得DF=HE,然后根据HE=AE-AH=BC-CD,BC-CF=BC-(CD-DF)=2HE,判断出④正确.
解:∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE=![]() AB,
AB,
∵AD=![]() AB,
AB,
∴AE=AD,
在△ABE和△AHD中,
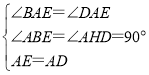 ,
,
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED=![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠CED=180°-45°-67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵AB=AH,
∵∠AHB=![]() (180°-45°)=67.5°,∠OHE=∠AHB(对顶角相等),
(180°-45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,
∴OE=OH,
∵∠DHO=90°-67.5°=22.5°,∠ODH=67.5°-45°=22.5°,
∴∠DHO=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°-67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,
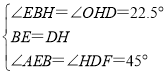 ,
,
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
∵HE=AE-AH=BC-CD,
∴BC-CF=BC-(CD-DF)=BC-(CD-HE)=(BC-CD)+HE=HE+HE=2HE.故④正确;
综上所述,结论正确的是①②③④共4个.
故选:D.

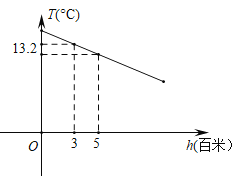
【题目】随着国内疫情基本得到控制,旅游业也慢慢复苏,经市场调研发现旅游景点未来![]() 天内,旅游人数
天内,旅游人数![]() 与时间
与时间![]() 的关系如下表;每张门票
的关系如下表;每张门票![]() 与时间
与时间![]() 之间存在如下图所示的一次函数关系.(
之间存在如下图所示的一次函数关系.(![]() ,且
,且![]() 为整数)
为整数)
时间 |
|
|
|
|
|
人数 |
|
|
|
|
|
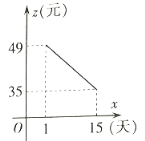
请结合上述信息解决下列问题:
(1)直接写出:![]() 关于
关于![]() 的函数关系式是 .
的函数关系式是 .![]() 与时间
与时间![]() 函数关系式是 .
函数关系式是 .
(2)请预测未来![]() 天中哪一天的门票收入最多,最多是多少?
天中哪一天的门票收入最多,最多是多少?
(3)为支援武汉抗疫,该旅游景点决定从每天获得的门票收入中拿出![]() 元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于
元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于![]() 元?
元?