题目内容
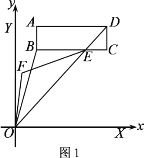
【题目】如图，长方形ABCD在平面直角坐标系中，点A（1，8），B（1，6），C（7，6），点X，Y分别在x，y轴上.
（1）请直接写出D点的坐标 ；
（2）连接OB、OD，OD交BC于点E，∠BOY的平分线和∠BEO的平分线交于点F，若∠BOE＝n，求∠OFE的度数.
（3）若长方形ABCD以每秒
个单位的速度向下运动，设运动时间为t秒，问在第一象限内是否存在某一时刻t，使△OBD的面积等于长方形ABCD的面积的
？若存在，请求出t的值，若不存在，请说明理由。
【答案】（1）（7，8）；（2）∠EFO＝135°－
n；（3）存在，t＝2.
【解析】
（1）由长方形的性质得出AB=DC，AD=BC，由题意得出AB=DC=2，即可得出D点的坐标；
（2）设∠BEO=2x，则∠EOX=2x，作FG∥OX，得出
，由角平分线得出
，得出
，由平行线得出∠EFG=∠BEF=x，得出
，即可得出∠OFE的度数；
（3）作AM⊥y轴于M，先求出矩形ABCD的面积，△OBD的面积=△ODM的面积-△ABD的面积-梯形AMOB的面积，得出方程，解方程即可求出t的值．
解：（1）∵四边形ABCD是长方形，
∴AB=DC，AD=BC，
∵点A（1，8），B（1，6），C（7，6），
∴AB=DC=2，
∴D点的坐标为：（7，8）；
故答案为：（7，8）；
（2）∵∠BOY的平分线和∠BEO的平分线交于点F，
∵BC∥OX，
∴∠BEO=∠EOX，
设∠BEO=2x，
则∠EOX=2x，
作FG∥OX，如图1所示：
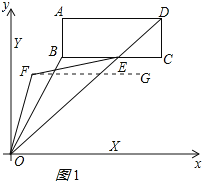
则
又
∵BC∥FG∥OX，
∴∠EFG=∠BEF=x，
（3）存在某一时刻，使△OBD的面积等于长方形ABCD面积的
，t=2；理由如下：
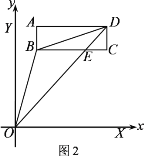
作AM⊥y轴于M，如图2所示：
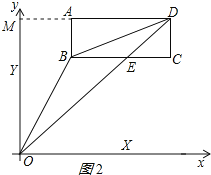
∵S矩形ABCD=2×6=12，
S△OBD=S△ODM-S△ABD-S梯形AMOB= 
解得：t=2．
