题目内容
【题目】已知一次函数y=ax+b的图象上有两点A、B,它们的横坐标分别是3,-1,若二次函数y=![]() x2的图象经过A、B两点.
x2的图象经过A、B两点.
(1)请求出一次函数的表达式;
(2)设二次函数的顶点为C,求△ABC的面积.
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】
试题分析:(1)将A、B的横坐标代入抛物线的解析式中,即可求得A、B的坐标,然后将它们代入直线的解析式中,可得方程组,解方程组即可求得a、b的值,从而得一次函数的表达式;(2)抛物线y=![]() x2的顶点是原点O,设直线AB与x轴的交点为D,先根据直线AB的解析式求出D点坐标,然后根据△ADO的面积减去△OBD的面积=△OAB的面积即可求得.
x2的顶点是原点O,设直线AB与x轴的交点为D,先根据直线AB的解析式求出D点坐标,然后根据△ADO的面积减去△OBD的面积=△OAB的面积即可求得.
△OAB的面积.
试题解析:解:(1)设A点坐标为(3,m);B点坐标为(-1,n).
∵A、B两点在y=x2的图象上,∴m=![]() ×9=3,
×9=3,
n=![]() ×1=
×1=![]() .
.
∴A(3,3),B(-1,![]() ).
).
∵A、B两点又在y=ax+b的图象上,可得,
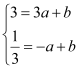 ,解得
,解得![]()
∴一次函数的表达式是![]() .
.
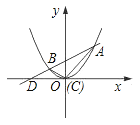
(2)如下图,设直线AB与x轴的交点为D,则D点坐标为(![]() ,0),
,0),
S△ABC=S△ADC-S△BDC=![]() ×
×![]() ×3-
×3-![]() ×
×![]() ×1=2.
×1=2.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目