题目内容
【题目】请认真观察图形,解答下列问题:
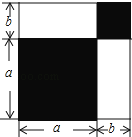
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
【答案】(1)a2+b2或 (a+b)2﹣2ab;(2)a2+b2=(a+b)2﹣2ab;(3)①9,②2385
【解析】
试题分析:(1)直接把两个正方形的面积相加或利用大正方形的面积减去两个长方形的面积;
(2)利用面积相等把(1)中的式子联立即可;
(3)注意a,b都为正数且a>b,利用(2)的结论进行探究得出答案即可.
解:(1)两个阴影图形的面积和可表示为:
a2+b2或 (a+b)2﹣2ab;
(2)a2+b2=(a+b)2﹣2ab;
(3)∵a,b(a>b)满足a2+b2=53,ab=14,
∴①(a+b)2=a2+b2+2ab
=53+2×14=81
∴a+b=±9,
又∵a>0,b>0,∴a+b=9.
![]()
②∵a4﹣b4=(a2+b2)(a+b)(a﹣b),
且∴a﹣b=±5
又∵a>b>0,
∴a﹣b=5,
∴a4﹣b4=(a2+b2)(a+b)(a﹣b)=53×9×5=2385.

练习册系列答案
相关题目