题目内容
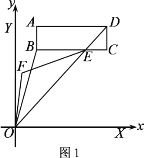
【题目】已知,正方形![]() 中,点E在
中,点E在![]() 上,点F在
上,点F在![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() .且
.且![]() 平分
平分![]() .
.

(1)如图1,求证:![]() .
.
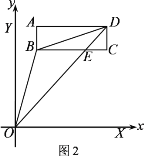
(2)如图2,若点E为BC的中点,![]() ,求
,求![]() 的面积.
的面积.
(3)如图3,若∠B=90°,连接BD分别交AF、AE于M、N两点,连接ME,若ME⊥AF于M, BM:EF=4![]() :5,△AEF的面积为15时,求AE的长度.
:5,△AEF的面积为15时,求AE的长度.
【答案】(1)证明见解析;(2)15;(3)2![]() .
.
【解析】
(1)作AH⊥EF于H.只要证明△AFD≌△AFH,推出∠FAD=∠FAH,同法可证:∠EAB=∠EAH,由此即可解决问题;
(2)由△EAB≌△EAH,△FAD≌△FAH,推出BE=EH=3,DF=FH,设DF=FH=x,在Rt△EFC中,根据EF2=EC2+CF2,可得(x+3)2=32+(6-x)2,推出x=2,推出EF=3+2=5,即可解决问题;
(3)如图3中,如图将△ADM顺时针旋转90°得到△ABK.首先证明MN2=BN2+DM2,再证明EF=![]() MN,由BM:EF=4
MN,由BM:EF=4![]() :5,推出BM:
:5,推出BM:![]() MN=4
MN=4![]() :5,推出BM:NM=8:5,设BM=8k,NM=5k,则BN=3k,DM=
:5,推出BM:NM=8:5,设BM=8k,NM=5k,则BN=3k,DM=![]() =4k,由DF∥AB,推出
=4k,由DF∥AB,推出![]() =2,设MF=y,则AM=ME=2y,由
=2,设MF=y,则AM=ME=2y,由![]() AFEM=15,推出
AFEM=15,推出![]() 3b2b=15,可得b=
3b2b=15,可得b=![]() ,由此即可解决问题.
,由此即可解决问题.
(1)证明:作AH⊥EF于H.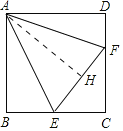
∵四边形ABCD是正方形,
∴∠B=∠D=∠BAD=90°,AB=AD=BC=CD,
∵AE平分∠BEF,AB⊥BE,AH⊥EF,
∴AB=AH=AD,
在Rt△AFD和Rt△AFH中,![]() ,
,
∴△AFD≌△AFH,
∴∠FAD=∠FAH,同法可证:∠EAB=∠EAH,
∴∠EAF=![]() ∠BAH+
∠BAH+![]() ∠DAH=
∠DAH=![]() ×90°=45°.
×90°=45°.
(2)解:∵△EAB≌△EAH,△FAD≌△FAH,
∴BE=EH=3,DF=FH,设DF=FH=x,
在Rt△EFC中,∵EF2=EC2+CF2,
∴(x+3)2=32+(6-x)2,
∴x=2,
∴EF=3+2=5,
∴S△AEF=![]() ×5×6=15.
×5×6=15.
(3)解:如图3中,如图将△ADM顺时针旋转90°得到△ABK.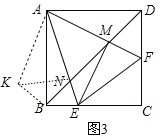
∵∠BAD=90°,∠MAN=45°,
∴∠DAM+∠BAN=45°,
∵∠DAM=∠BAK,
∴∠BAN+∠BAK=45°,
∴∠NAK=∠MAN=45°,
∵AN=AN,AK=AM,
∴△ANK≌△ANM,
∴MN=KN,
∵∠ABK=∠ADM=45°=∠ABD,
∴∠KBN=90°,
∴KN2=BN2+BK2,
∵DM=BK,
∴MN2=BN2+DM2,
∵∠MAN=∠NBE,∠ANM=∠BNE,
∴∠AMN=∠BEN=∠AEF,
∵∠AMN=∠EAF,
∴△AMN∽△AEF,
∴![]() ,
,
∴EF=![]() MN,
MN,
∵BM:EF=4![]() :5,
:5,
∴BM:![]() MN=4
MN=4![]() :5,
:5,
∴BM:NM=8:5,设BM=8k,NM=5k,
则BN=3k,DM=![]() =4k,
=4k,
∵DF∥AB,
∴![]() =2,设MF=y,则AM=ME=2y,
=2,设MF=y,则AM=ME=2y,
∵![]() AFEM=15,
AFEM=15,
∴![]() 3b2b=15,
3b2b=15,
∴b2=5,
∵b>0,
∴b=![]() ,
,
∴AM=EM=2![]() ,
,
∴AE=![]() AM=2
AM=2![]() .
.

 天天练口算系列答案
天天练口算系列答案