题目内容
解方程:(每小题6分,共12分)
(1)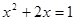 (2)
(2)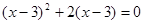
(1)
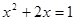 (2)
(2)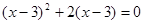
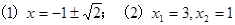
观察式子特点确定求解方法:
(1)用配方法求解,首先把二次项系数化为1,然后把常数项移到等号的右边,方程两边同时加上一次项系数的一半即可转化为左边是完全平方式,右边是常数的形式,即可求解;
(2)因式分解法求解,移项以后可以提取公因式x-3,则转化为两个因式的积是0的形式,即可转化为两个一元一次方程求解.
解:(1)x2+2x-1=0
x2+2x+1-1-1=0
x2+2x+1=2
(x+1)2=2
∴x1=-1+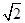 ,x2=-1-
,x2=-1-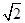 ;
;
(2)(x-3)2+2(x-3)=0
∴(x-3)(x-3+2)=0
∴x-3=0或x-1=0,
∴x1=3,x2=1.
(1)用配方法求解,首先把二次项系数化为1,然后把常数项移到等号的右边,方程两边同时加上一次项系数的一半即可转化为左边是完全平方式,右边是常数的形式,即可求解;
(2)因式分解法求解,移项以后可以提取公因式x-3,则转化为两个因式的积是0的形式,即可转化为两个一元一次方程求解.
解:(1)x2+2x-1=0
x2+2x+1-1-1=0
x2+2x+1=2
(x+1)2=2
∴x1=-1+
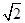 ,x2=-1-
,x2=-1-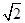 ;
;(2)(x-3)2+2(x-3)=0
∴(x-3)(x-3+2)=0
∴x-3=0或x-1=0,
∴x1=3,x2=1.

练习册系列答案
相关题目
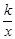 的图象经过点P(a、b),其中a、b是一元二次方程x2+kx+4=0的两根,那么点P的坐标是________.
的图象经过点P(a、b),其中a、b是一元二次方程x2+kx+4=0的两根,那么点P的坐标是________.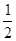
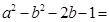 .
.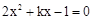 .
.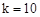 时,方程的两根之和为 ,两根之积为
时,方程的两根之和为 ,两根之积为 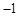 ,求
,求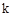 的值;
的值;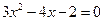 .
. 的方程
的方程 有增根,则
有增根,则 的值是 .
的值是 . 的解为 .
的解为 .