题目内容
若关于x的方程x2+2(k一l)x+k2=0有实数根,则k的取值范围是
A.k<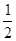 | B.k≤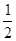 | C.k>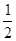 | D.k≥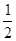 |
B
分析:根据一元二次方程的根的判别式与根的关系,建立关于k的不等式,然后就可以求出k的取值范围.
解答:解:∵a=1,b=2(k-1),c=k2,
而方程有实数根,
∴△=b2-4ac
=4(k-1)2-4k2=4-8k≥0,
∴k≤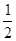 .
.
故选B.
解答:解:∵a=1,b=2(k-1),c=k2,
而方程有实数根,
∴△=b2-4ac
=4(k-1)2-4k2=4-8k≥0,
∴k≤
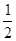 .
.故选B.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
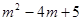 的值是一个( )
的值是一个( )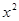 -3x-2=0
-3x-2=0 的一个常数m的值是 。
的一个常数m的值是 。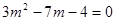 (配方法) (2)
(配方法) (2)

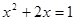 (2)
(2)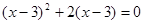
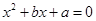 有一个根是
有一个根是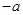
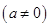 ,则代数式
,则代数式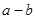 的值是
的值是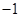
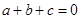 ,则
,则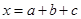 是一元二次方程
是一元二次方程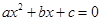 的一个根
的一个根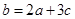 ,则一元二次方程
,则一元二次方程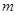 取整数
取整数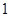 时,关于
时,关于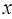 的一元二次方程
的一元二次方程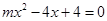 与
与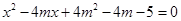 的解都是整数。
的解都是整数。 个
个 个
个 个
个