题目内容
已知:关于x的方程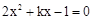 .
.
(I)求证:方程有两个不相等的实数根;
(II)当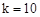 时,方程的两根之和为 ,两根之积为
时,方程的两根之和为 ,两根之积为
(III)若方程的一个根是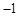 ,求
,求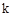 的值;
的值;
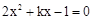 .
.(I)求证:方程有两个不相等的实数根;
(II)当
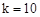 时,方程的两根之和为 ,两根之积为
时,方程的两根之和为 ,两根之积为 (III)若方程的一个根是
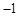 ,求
,求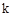 的值;
的值;(1)证明△>0;(2)-5,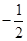 ;(3)1
;(3)1
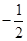 ;(3)1
;(3)1分析:
(1)求出△的取值范围,再根据一元二次方程根的判别式与方程根的关系即可解答;
(2)把k=10代入原方程,由根与系数的关系即可得出两根之和与两根之积;
(3)把x=-1代入原方程即可求出k的值。
解答:
(1)∵△=k2+8>0,
∴方程有两个不相等的实数根;
(2)当k=10时,原方程可化为2x2+10x-1=0,
∴方程的两根之和=-10/2=-5,两根之积=-1/2;
(3)把x=-1代入方程2x2+kx-1=0得,2-k-1=0,解得k=1。
点评:本题考查的是根与系数的关系及根的判别式,解答此题时要熟知一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系,即当△>0时,方程有两个不相等的两个实数根。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 的一个常数m的值是 。
的一个常数m的值是 。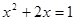 (2)
(2)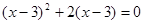
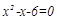 的根是( )
的根是( )



 ,
, ,且
,且 ,则
,则 的值为
的值为 ”部分所对应的圆心角的度数是 ;
”部分所对应的圆心角的度数是 ;

 图,要建一个面积为40平方米的矩形花园ABCD,为了节约材料,花园的一边AD靠着原有的一面墙,墙长为8米(AD<8),另三边用栅栏围成,已知栅栏总长为24米,求花园一边AB的长.
图,要建一个面积为40平方米的矩形花园ABCD,为了节约材料,花园的一边AD靠着原有的一面墙,墙长为8米(AD<8),另三边用栅栏围成,已知栅栏总长为24米,求花园一边AB的长.