��Ŀ����
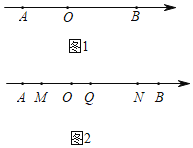
����Ŀ����֪��A�������϶�Ӧ����Ϊa����B��Ӧ����Ϊb����|a+2|+��b��1��2=0��A��B֮��ľ������|AB|�����壺|AB|=|a��b|��
���߶�AB�ij�|AB|=3��
�����P�������϶�Ӧ����Ϊx����|PA|��|PB|=2ʱ��x=0.5��
������P��A����࣬M��N�ֱ���PA��PB���е㣬��P��A������ƶ�ʱ|PM|+|PN|��ֵ���䣻
�������������£�|PN|��|PM|��ֵ���䣮
�����٢ڢۢ���������ȷ����_______������������ȷ���۵���ţ�
���𰸡��٢ڢ�
����������1�����ݷǸ����ĺ�Ϊ0�����Ϊ0��
��2��Ӧ���ǵ�A��B��P����֮���λ�ù�ϵ�Ķ��ֿ��ܽ��⣻
��3��(4)�����е�����ת���߶�֮��ı��ֹ�ϵ�ó���
��1����|a+2|+��b-1��2=0��
��a=-2��b=1��
��AB=|a-b|=3�����߶�AB�ij���Ϊ3��
��2����P�ڵ�A���ʱ��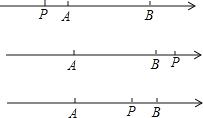
|PA|-|PB|=-��|PB|-|PA|��=-|AB|=-3��2��
��P�ڵ�B�Ҳ�ʱ��
|PA|-|PB|=|AB|=3��2��
��������������ĵ�P�����ڣ�
��P��A��B֮��ʱ��-2��x��1��
��|PA|=|x+2|=x+2��|PB|=|x-1|=1-x��
����|PA|-|PB|=2����x+2-��1-x��=2��
���ã�x=0.5��
��3������֪�ɵó���PM=![]() PA��PN=
PA��PN=![]() PB��
PB��
|PM|+|PN|= ![]() ��PA+PB��= PA+
��PA+PB��= PA+![]() AB
AB
���ԣ�|PM|+|PN|��ֵ��P��λ�ñ仯���仯.
(4) �ڣ�3�������£�|PN|��|PM|=![]() PB-
PB-![]() PA=
PA=![]() ��PB-PA��=
��PB-PA��=![]() AB=
AB=![]()
�ۺ��������٢ڢ�˵����ȷ.
�ʴ�Ϊ���٢ڢ�.

����Ŀ����10�֣������ͼ�����ɱ߳�Ϊl�������ΰ���ij�ֹ������ж���ɵģ�
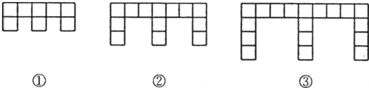
��1���۲�ͼ�Σ���д�±���
ͼ�� | �� | �� | �� |
�����εĸ��� | 8 | �� �� | �� �� |
ͼ�ε��ܳ� | 18 | �� �� | �� �� |
��2���Ʋ��n��ͼ���У������εĸ���Ϊ�� �����ܳ�Ϊ�� �������ú�n�Ĵ���ʽ��ʾ����
��3����Щͼ���У�����һ��ͼ�ε��ܳ�y�������������θ���x֮��Ĺ�ϵ�ɱ�ʾΪy=�� ����