��Ŀ����
����Ŀ����֪��b����С����������a��b����![]() ���Իش�����.
���Իش�����.
��1����ֱ��д��a��b��c��ֵ.
a= b= c= .
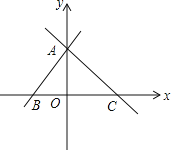
��2��a��b��c����Ӧ�ĵ�ֱ�ΪA��B��C����PΪһ���㣬���Ӧ����Ϊx����P��0��2֮���˶�ʱ����0��x��2ʱ�����뻯��ʽ�ӣ�![]() ����д��������̣�
����д��������̣�
![]()
��3���ڣ�1����2���������£�����D��A�㿪ʼ��ÿ��1���ٶ������˶���ͬʱ��E��B�㿪ʼ��ÿ��2����λ���������˶�����F��C�㿪ʼ��ÿ��5����λ���ȵ��ٶ������˶����������˶���t�룬���ʣ�EF��DE��ֵ�Ƿ�����ʱ��t�ı仯���仯�����仯����˵�����ɣ������䣬������ֵ.
���𰸡���1��a=-1��b=1��c=5����2������Ϊ![]() ����3�����䣬EF��DE��ֵΪ2
����3�����䣬EF��DE��ֵΪ2
��������
��1������b����С��������������ȷ��b��ֵ��Ȼ����ݷǸ��������ʣ������Ǹ�����ʽ���ĺ���0����ÿ������ʽ����0���������a��b��c��ֵ��
��2������x�ķ�Χ���ֱ�ȷ��x+1��x-1��x-5�ķ��ţ�Ȼ����ݾ���ֵ�����弴�ɻ���
��3������D��E��F���˶��������ȷ��DE��EF�ı仯���������ȷ��EF-DE��ֵ��
�⣺��1����b����С����������
��b=1��
��![]()
��c-5=0��a+b=0��
��a=-1��b=1��c=5��
��2����������ɵ�
0��x��2����x-1=0ʱ��x=1
�ٵ�0��x��1ʱ��ԭʽ=��x+1��+��x-1��+2��5-x��=10��
�ڵ�1��x��2ʱ��ԭʽ=��x+1��-��x-1��+2��5-x��=-2x+12��
�ʻ���Ϊ![]() ��
��
��3�����䣮
�ߵ�D��ÿ��1����λ���ȵ��ٶ������˶�����Eÿ��2����λ���������˶���
��D��Eÿ��������3����λ���ȣ�
�ߵ�E�͵�F�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶���
��E��Fÿ��������3����λ���ȣ�
��EF-DE=2��EF-DE��ֵ������ʱ��t�ı仯���ı䣮