��Ŀ����
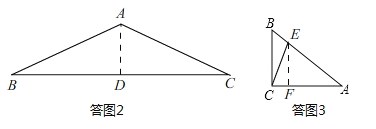
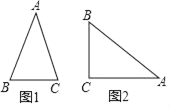
����Ŀ�������Ķ��������ڽ̲�24.3�Ѿ�֪����ֱ������������ǵ����Ǻ����ĸ�����Ƶأ������ڵ����������н����߽�֮��Ĺ�ϵ���������������еױ������ıȽ������ǵ����ԣ�������sad����ͼ1������ABC�У�AB=AC������A�����Լ�����sadA����ʱsadA=![]() =
=![]() ��
��
��������
��1��������A=60������sadA��ֵ��
��2����90�㣼��A��180�������A������sadA��ȡֵ��Χ��
����������
��3����ͼ2����Rt��ABC�У���ACB=90������sinA=![]() ��������ACΪ���ĵ����������У�����A������sadA��ֵ��
��������ACΪ���ĵ����������У�����A������sadA��ֵ��
���𰸡���1��1����2��![]() ��sad��BAC��2����3��
��sad��BAC��2����3��![]() .
.
����������������1�����жϳ���ABC�ǵȱ��������������ó�BC=AC�����ɵó�������
��2�����жϳ�![]() ��sin��BAD��1�������ó�
��sin��BAD��1�������ó�![]() ��
��![]() ��2�����ɵó�������
��2�����ɵó�������
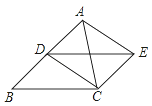
��3�������BC=3a���ó�AB=5a��AC=4a�������ó�AE=AC=4a�����жϳ���AEF�ס�ABC���ó�EF=![]() a��AF=
a��AF=![]() a��������ʾ��CF=AC��AF=
a��������ʾ��CF=AC��AF=![]() a�����ù��ɶ����ó�CE=
a�����ù��ɶ����ó�CE=![]() a���ɵó����ۣ�
a���ɵó����ۣ�
�������1���ߵ��������εĶ���A=60�㣬���ABC�ǵȱ�����������BC=AC����sadA=![]() =1��
=1��
��2�����ͼ2������A��AD��BC��D����AB=AC����BC=2BD����90������BAC��180�㣬��45������BAD��90�㣬��![]() ��sin��BAD��1����Rt��ABD����sin��BAD=
��sin��BAD��1����Rt��ABD����sin��BAD=![]() ��
��![]() ��1����
��1����![]() ��
��![]() ��2����
��2����![]() ��
��![]() ��2���ڵ�����ABC����sad��BAC=
��2���ڵ�����ABC����sad��BAC=![]() ��sad��BAC��2��
��sad��BAC��2��
��3�����ͼ3����Rt��ABC����sinA=![]() =
=![]() ����BC=3a����AB=5a�����ݹ��ɶ�������AC=4a����AE=AC=4a������E��EF��AC��F���ߡ�ACB=90�㣬��EF��BC�����AEF�ס�ABC����
����BC=3a����AB=5a�����ݹ��ɶ�������AC=4a����AE=AC=4a������E��EF��AC��F���ߡ�ACB=90�㣬��EF��BC�����AEF�ס�ABC����![]() ����EF=
����EF=![]() a��AF=
a��AF=![]() a����CF=AC��AF=
a����CF=AC��AF=![]() a����Rt��CEF����CE=
a����Rt��CEF����CE=![]() =
=![]() a����sadA=
a����sadA=![]() =
=![]() =
=![]() ��
��