题目内容
【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
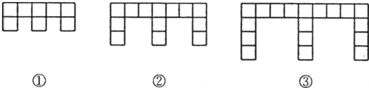
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
【答案】(1)②13,28;③18,38;(2)5n+3;10+8;(3)2x+2
【解析】试题分析:(1)依此数出n=1,2,3,…,正方形的个数,算出图形的周长;
(2)根据规律以此类推,可得出第n个图形中,正方形的个数为及周长;
(3)根据上问规律,得出y与x之间的关系.
试题解析:(1)∵n=1时,正方形有8个,即8=5×1+3,周长是18,即18=10×1+8;
n=2时,正方形有13个,即13=5×2+3,周长是28,即28=10×2+8;
n=3时,正方形有18个,即18=5×3+3,周长是38,即38=10×3+8;
(2)由(1)可知,n=n时,正方形有5n+3个,周长是10n+8.
(3)∵y=10n+8,x=5n+3,
∴y=2x+2.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目