╠Ō─┐─┌╚▌
ĪŠ╠Ō─┐Ī┐ęčų¬ĄŃ![]() į┌╩²ųß╔ŽČįė”Ą─╩²╬¬
į┌╩²ųß╔ŽČįė”Ą─╩²╬¬![]() Ż¼ĄŃ
Ż¼ĄŃ![]() Čįė”Ą─╩²╬¬
Čįė”Ą─╩²╬¬![]() Ż¼╣žė┌
Ż¼╣žė┌![]() Ż¼
Ż¼![]() Ą─ČÓŽŅ╩Į
Ą─ČÓŽŅ╩Į![]() ╩Ū6┤╬ČÓŽŅ╩ĮŻ¼Ūę│Ż╩²ŽŅ╬¬-6.
╩Ū6┤╬ČÓŽŅ╩ĮŻ¼Ūę│Ż╩²ŽŅ╬¬-6.
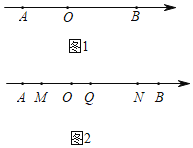
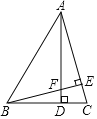
Ż©1Ż®ĄŃ![]() ĄĮ
ĄĮ![]() Ą─ŠÓ└ļ╬¬______Ż©ų▒Įėą┤│÷Įß╣¹Ż®Ż╗
Ą─ŠÓ└ļ╬¬______Ż©ų▒Įėą┤│÷Įß╣¹Ż®Ż╗
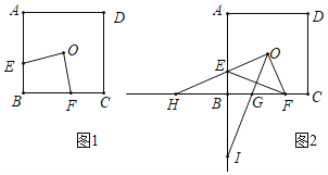
Ż©2Ż®╚ń═╝1Ż¼ĄŃ![]() ╩Ū╩²ųß╔Žę╗ĄŃŻ¼ĄŃ
╩Ū╩²ųß╔Žę╗ĄŃŻ¼ĄŃ![]() ĄĮ
ĄĮ![]() Ą─ŠÓ└ļ╩Ū
Ą─ŠÓ└ļ╩Ū![]() ĄĮ
ĄĮ![]() Ą─ŠÓ└ļĄ─3▒ČŻ©╝┤
Ą─ŠÓ└ļĄ─3▒ČŻ©╝┤![]() Ż®Ż¼Ū¾ĄŃ
Ż®Ż¼Ū¾ĄŃ![]() į┌╩²ųß╔ŽČįė”Ą─╩²Ż╗
į┌╩²ųß╔ŽČįė”Ą─╩²Ż╗
Ż©3Ż®╚ń═╝2Ż¼ĄŃ![]() Ż¼
Ż¼![]() Ęų▒┤ėĄŃ
Ęų▒┤ėĄŃ![]() Ż¼
Ż¼![]() ═¼╩▒│÷ĘóŻ¼Ęų▒ęį
═¼╩▒│÷ĘóŻ¼Ęų▒ęį![]() Ż¼
Ż¼![]() Ą─╦┘Č╚čž╩²ųßĖ║ĘĮŽ“į╦Č»Ż©
Ą─╦┘Č╚čž╩²ųßĖ║ĘĮŽ“į╦Č»Ż©![]() į┌
į┌![]() Ż¼
Ż¼![]() ų«╝õŻ¼
ų«╝õŻ¼![]() į┌
į┌![]() Ż¼
Ż¼![]() ų«╝õŻ®Ż¼į╦Č»╩▒╝õ╬¬
ų«╝õŻ®Ż¼į╦Č»╩▒╝õ╬¬![]() Ż¼ĄŃ
Ż¼ĄŃ![]() ╬¬
╬¬![]() Ż¼
Ż¼![]() ų«╝õę╗ĄŃŻ¼ŪęĄŃ
ų«╝õę╗ĄŃŻ¼ŪęĄŃ![]() ĄĮ
ĄĮ![]() Ą─ŠÓ└ļ╩ŪĄŃ
Ą─ŠÓ└ļ╩ŪĄŃ![]() ĄĮ
ĄĮ![]() ŠÓ└ļĄ─ę╗░ļŻ©╝┤
ŠÓ└ļĄ─ę╗░ļŻ©╝┤![]() Ż®Ż¼╚¶
Ż®Ż¼╚¶![]() Ż¼
Ż¼![]() į╦Č»╣²│╠ųą
į╦Č»╣²│╠ųą![]() ĄĮ
ĄĮ![]() Ą─ŠÓ└ļŻ©╝┤
Ą─ŠÓ└ļŻ©╝┤![]() Ż®ū▄╬¬ę╗Ė÷╣╠Č©Ą─ųĄŻ¼Ū¾
Ż®ū▄╬¬ę╗Ė÷╣╠Č©Ą─ųĄŻ¼Ū¾![]() Ą─ųĄ.
Ą─ųĄ.
ĪŠ┤░ĖĪ┐Ż©1Ż®8Ż╗Ż©2Ż®![]() ╗“9Ż╗Ż©3Ż®
╗“9Ż╗Ż©3Ż®![]() .
.
ĪŠĮŌ╬÷Ī┐
Ż©1Ż®Ė∙Š▌ČÓŽŅ╩ĮĄ─┤╬╩²║═│Ż╩²ŽŅ╝┤┐╔Ū¾ĮŌŻ╗
Ż©2Ż®Ė∙Š▌┴ĮĄŃų«╝õĄ─ŠÓ└ļ┴ąĄ╚╩Į╝┤┐╔Ū¾ĮŌŻ╗
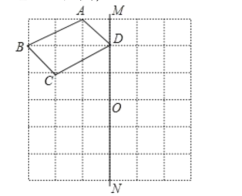
Ż©3Ż®Ė∙Š▌Č»ĄŃį╦Č»╦┘Č╚║═╩▒╝õ▒Ē╩ŠŽ▀Č╬Ą─│żŻ¼į┘Ė∙Š▌QĄĮMĄ─ŠÓ└ļŻ©╝┤QMŻ®ū▄╬¬ę╗Ė÷╣╠Č©Ą─ųĄėļtųĄ╬▐╣ž╝┤┐╔Ū¾ĮŌŻ«
ĮŌŻ║Ż©1Ż®Ė∙Š▌╠ŌęŌŻ¼Ą├
2a=-6Ż¼ĮŌĄ├a=-3Ż¼b=5Ż«
╦∙ęįĄŃA▒Ē╩ŠĄ─╩²╬¬-3Ż¼ĄŃB▒Ē╩ŠĄ─╩²╬¬5Ż¼
╦∙ęįAĪóBų«╝õĄ─ŠÓ└ļ╬¬8Ż«
╣╩┤░Ė╬¬8Ż«
Ż©2Ż®╔ĶĄŃ![]() Čįė”Ą─╩²╬¬
Čįė”Ą─╩²╬¬![]() Ż¼ę└╠ŌęŌĄ├Ż║
Ż¼ę└╠ŌęŌĄ├Ż║
![]() Ż¼
Ż¼
ĮŌĄ├![]() ╗“9Ż╗
╗“9Ż╗
Ż©3Ż®ę└╠ŌęŌŻ║![]() Ż¼
Ż¼![]() Ż¼
Ż¼
ĪÓ![]() Ż¼
Ż¼![]() Ż¼
Ż¼
Ī▀![]()
ĪÓ![]() Ż¼
Ż¼
ĪÓ![]() Ż¼
Ż¼
ę“╬¬![]() Ż¼
Ż¼![]() į╦Č»╣²│╠ųą
į╦Č»╣²│╠ųą![]() ĄĮ
ĄĮ![]() Ą─ŠÓ└ļŻ©╝┤
Ą─ŠÓ└ļŻ©╝┤![]() Ż®ū▄╬¬ę╗Ė÷╣╠Č©Ą─ųĄŻ¼
Ż®ū▄╬¬ę╗Ė÷╣╠Č©Ą─ųĄŻ¼
╝┤![]() Ą─ųĄėļ
Ą─ųĄėļ![]() ╬▐╣žŻ¼
╬▐╣žŻ¼
╝┤![]() Ż¼
Ż¼![]() Ż¼
Ż¼
ĪÓ![]() .
.