题目内容
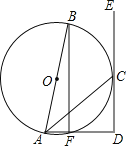
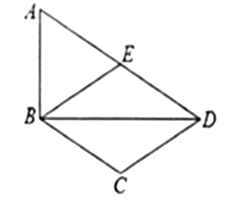
【题目】如图,在四边形ABCD中,BD为一条对角线,![]() 且
且![]() ,
,![]() ,E为AD的中点,连接BE.
,E为AD的中点,连接BE.
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分![]() ,
,![]() ,求AC的长.
,求AC的长.
【答案】(1)详见解析(2)![]()
【解析】
(1) 题干中由![]() 且
且![]() 可知,一组对边平行且相等的四边形是平行四边形,则四边形BCDE是平行四边形,又知BE是直角三角形斜边的中线,直角三角形斜边的中线等于斜边的一半,则得到BE=ED,从而再用一组邻边相等的平行四边形是菱形证明即可.
可知,一组对边平行且相等的四边形是平行四边形,则四边形BCDE是平行四边形,又知BE是直角三角形斜边的中线,直角三角形斜边的中线等于斜边的一半,则得到BE=ED,从而再用一组邻边相等的平行四边形是菱形证明即可.
(2)通过 DE∥BC和 AC平分![]() ,可得到∠BAC=∠ACB,从而由等角对等边得到AB=BC=1,则此时直角三角形ABD,有一个执教不是斜边的一半,则可知这个直角边对应的角是30°,找到30°才是题目的突破口,然后依次得到角度的关系,证明得到三角形ACD是直角三角形,再用勾股定理解得AC的长.
,可得到∠BAC=∠ACB,从而由等角对等边得到AB=BC=1,则此时直角三角形ABD,有一个执教不是斜边的一半,则可知这个直角边对应的角是30°,找到30°才是题目的突破口,然后依次得到角度的关系,证明得到三角形ACD是直角三角形,再用勾股定理解得AC的长.
(1)证明:∵DE∥BC且DE=BC(已知)
∴四边形BCDE是平行四边形(一组对边平行且相等的四边形是平行四边形)
又∵E为直角三角形斜边AD边的中点(已知)
∴BE=![]() AD,即BE=DE(直角三角形斜边的中线等于斜边的一半)
AD,即BE=DE(直角三角形斜边的中线等于斜边的一半)
∴平行四边形四边形BCDE是菱形(一组邻边相等的平行四边形是菱形)
(2)
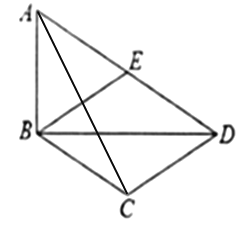
连接AC,如图可知:
∵DE∥BC(已知)
∴∠DAC=∠ACB(两直线平行内错角相等)
又∵AC平分![]() (已知)
(已知)
∴∠BAC=∠DAC(角平分线的定义)
即∠BAC=∠ACB(等量代换)
∴AB=BC=1(等角对等边)
由(1)可知:AD=2ED=2BC=2
在直角三角形中AB=1,AD=2
∴∠ADB=30°(直角三角形中,若一个直角边是斜边 一半,则这个直角边所对的角是30°)
∴∠BAD=60°(直角三角形两锐角互余)
即∠CAD=![]() ∠BAD=30°(角平分线的定义),∠ADC=2∠ADB=60°(菱形的性质)
∠BAD=30°(角平分线的定义),∠ADC=2∠ADB=60°(菱形的性质)
所以三角形ADC是直角三角形.
则由![]() 可知:
可知:
![]()

 活力课时同步练习册系列答案
活力课时同步练习册系列答案