题目内容
【题目】如图,平面直角坐标系中有![]() 三点。
三点。
(1)连接![]() ,若
,若![]()
①线段的长为 (直接写出结果)
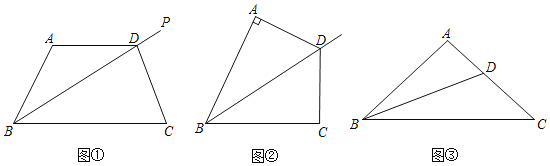
②如图1,点![]() 为
为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() 作
作![]() ,且
,且![]() ,当点
,当点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 点不变,
点不变,![]() 点随之运动,连接
点随之运动,连接![]() ,求线段
,求线段![]() 的中点
的中点![]() 的运动路径长;
的运动路径长;
(2)如图2,作![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 延长线于
延长线于![]() 于
于![]() .若
.若![]() ,且
,且![]() ,在平面内是否存在点
,在平面内是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,若存在,请求出点
为顶点的四边形是平行四边形,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)①![]() ②
②![]() (2)
(2)![]()
【解析】
(1)①由两点的距离公式可得出答案;
②分别作出点D运动到点A,B时的等腰直角三角形DCE,画出运动路径如图,求出E1,E2的坐标,即可求出E1E2的长,则答案可求出;
(2)连接BH,证明∠HBA=45°,过点H作HN⊥AB,求出H点坐标,再根据平行四边形的性质可求出M点坐标.
(1)①∵A(3,0),C(4,1),
∴AC=![]() .
.
故答案为:![]() .
.
②分别作出点D运动到点A,B时的等腰直角三角形DCE,画出运动路径如图,
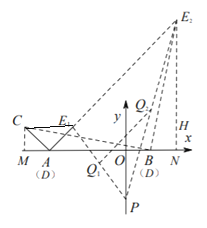
∵C(4,1),△CAE1为等腰直角三角形,A,D重合,A(-3,0)
∴CD=AC=![]() =AE1
=AE1
∴CE1=![]()
∵CE1∥x轴
∴E1(2,1),
分别过点C,E2作x轴的垂线,垂足分别为M,N,
∵∠CBM=∠BE2N,∠CMB=∠BNE2,BC=BE2,
∴△CMB≌△BNE2(AAS),
∴E2N=BM=5,CM=BN=1,
∴E2(2,5),
∴E1E2=![]() .
.
∵Q1Q2为△PE1E2的中位线,
∴线段EP的中点Q的运动路径长Q1Q2=![]() E1E2=2
E1E2=2![]() .
.
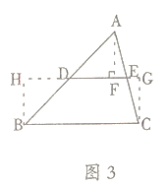
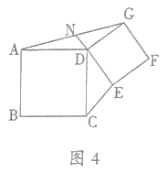
(2)如图,连接BH,
∵AF⊥AC,GH⊥CF,
又A(3,0),B(1,0),BF=BG,
∴BH=![]() GF=AB=4,
GF=AB=4,
又∵∠C=67.5°,
∴∠AGB+∠CFB=112.5°,
∴∠ABG+∠HBF=360°2(∠AGB+∠CFB)=135°,
即∠HBA=45°,
过点H作HN⊥AB,∴△BHN是等腰直角三角形,
∴HN=BN,
∴HN=BN=![]() BH=2
BH=2![]() ,
,
∴H(12![]() ,2
,2![]() ),
),
∵A(3,0),B(1,0),
如图,四边形ABM1H是平行四边形时,A平移至B的方式是:向右平移4个单位,
∴H点向右平移4个单位得到M1![]() ;
;
四边形ABH M2是平行四边形时,B平移至A的方式是:向左平移4个单位,
∴H点向右平移4个单位得到M2![]() ;
;
四边形AHBM3是平行四边形时,H平移至B的方式是:向右平移2![]() 个单位,向下平移2
个单位,向下平移2![]() 个单位,
个单位,
∴A点向右平移2![]() 个单位,向下平移2
个单位,向下平移2![]() 个单位M3
个单位M3![]() ;
;
∴使以B,A,H,M为顶点的四边形是平行四边形的点M的坐标为![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案