题目内容
【题目】综合与实践
问题背景:
我们知道,三角形的中位线平行于三角形的第三边,并且等于第三边的一半,如何证明三角形中位线定理呢?
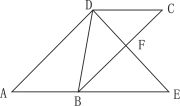
已知:如图1,在![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.

求证:![]()
问题中既要证明两条线段所在的直线平行,又要证明其中一条线段的长等于另一线段长的一半.所以可以用“倍长法”将![]() 延长一倍:延长
延长一倍:延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() 这样只需证明
这样只需证明![]() ,且
,且![]() .由于
.由于![]() 是
是![]() 的中点,容易证明四边形
的中点,容易证明四边形![]() 、四边形
、四边形![]() 是平行四边形,证明...
是平行四边形,证明...
问题解决:
![]() 上述材料中“倍长法”体现的数学思想主要是_____. (填入选项前的字母代号即可)
上述材料中“倍长法”体现的数学思想主要是_____. (填入选项前的字母代号即可)
A.数形结合思想 B.转化思想 C.分类讨论思想 D.方程思想
![]() 证明四边形
证明四边形![]() 是平行四边形的依据是
是平行四边形的依据是

反思交流:
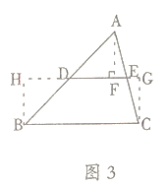
“智慧小组”在证明中位线定理时,在图1的基础上追加了如上辅助线作法:如图3,分别过点![]() 作
作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,..
,..
![]() 请你根据“智慧小组”添加的辅助线,证明三角形的中位线定理.
请你根据“智慧小组”添加的辅助线,证明三角形的中位线定理.
方法迁移:
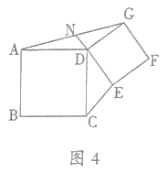
![]() 如图4、四边形
如图4、四边形![]() 和
和![]() 都是正方形,
都是正方形,![]() 是
是![]() 的中点.求证:
的中点.求证: ![]()
【答案】(1)B;(2)一组对边平行且相等的四边形是平行四边形;(3)详见解析;(4)详见解析
【解析】
(1)根据解题方法知,将证明“![]() ”的问题转化为矩形的性质的问题;
”的问题转化为矩形的性质的问题;
(2)由平行四边形的判定定理填空;
(3)利用“![]() ”证明
”证明![]() ,根据全等三角形对应边相等可得
,根据全等三角形对应边相等可得![]() ,
,![]() ,同理
,同理![]() ,
,![]() ,则
,则![]() .然后判断出四边形
.然后判断出四边形![]() 是矩形,根据矩形的性质即可得到答案;
是矩形,根据矩形的性质即可得到答案;
(4)如图4,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() 、
、![]() .易证,四边形
.易证,四边形![]() 是平行四边形,结合该平行四边形和图中正方形的性质,证得
是平行四边形,结合该平行四边形和图中正方形的性质,证得![]() ,故
,故![]() ,所以
,所以![]() .
.
(1)根据根据上述材料中“倍长法”体现的数学思想主要是转化思想.
故选:![]() ;
;
(2)证明四边形![]() 是平行四边形的依据是:一组对边平行且相等的四边形是平行四边形.
是平行四边形的依据是:一组对边平行且相等的四边形是平行四边形.
故答案为:一组对边平行且相等的四边形是平行四边形
(3)证明:如图3,

在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
同理可得![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() .
.
![]() 如图4,延长
如图4,延长![]() 到点
到点![]() ,使得
,使得![]() 连接
连接![]() ,
,![]() ,
,
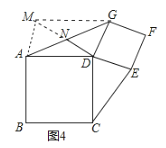
![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∴![]() ,
,
![]() 四边形
四边形![]() 和
和![]() 都是正方形,
都是正方形,
∴![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中
 ,
,
∴![]() ,
,
∴![]() ,
,
![]()

【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”、“3”、“3”、“5”、“6”的五张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖。记每次抽出两张牌点数之差为x,按表格要求确定奖项.
奖项 | 一等奖 | 二等奖 | 三等奖 |
|
|
|
|
(1)用列表或画树状图的方法求出某同学抽一次奖获一等奖的概率;
(2)抽一次奖获一等奖的概率和不获奖的概率相等吗?请说明理由.
【题目】某超市销售每台进价分别为180元、150元的甲、乙两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
甲种型号 | 乙种型号 | ||
第一周 | 2台 | 3台 | 1100元 |
第二周 | 4台 | 5台 | 2000元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求甲、乙两种型号的电器的销售单价;
(2)若超市准备用不多于5000元的金额再采购这两种型号的电器共30台,求甲种型号的电器最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电器能否实现利润超过1900元的目标?若能,请给出相应的采购方案;若不能,请说明理由.