题目内容
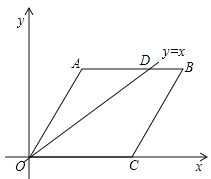
【题目】在平面直角坐标系中,菱形OABC的OC边落在x轴上,∠AOC=60°,OA=60![]() .若菱形OABC内部(边界及顶点除外)的一格点P(x,y)满足:x2﹣y2=90x﹣90y,就称格点P为“好点”,则菱形OABC内部“好点”的个数为( )
.若菱形OABC内部(边界及顶点除外)的一格点P(x,y)满足:x2﹣y2=90x﹣90y,就称格点P为“好点”,则菱形OABC内部“好点”的个数为( )
(注:所谓“格点”,是指在平面直角坐标系中横、纵坐标均为整数的点.)

A. 145 B. 146 C. 147 D. 148
【答案】A
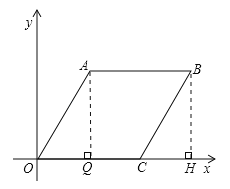
【解析】解:过A作AQ⊥OC于Q,过B作BH⊥X轴于H,∵∠A0C=60°,OA=![]() ,∴∠OAQ=30°,∴OQ=
,∴∠OAQ=30°,∴OQ=![]() ,由勾股定理得:AQ=90,∵x2﹣y2=90x﹣90y,∴(x﹣y)(x+y﹣90)=0,∴x=y,x+y=90,BH=90 OA:y′=
,由勾股定理得:AQ=90,∵x2﹣y2=90x﹣90y,∴(x﹣y)(x+y﹣90)=0,∴x=y,x+y=90,BH=90 OA:y′=![]() x
x
(1)y=x时,令y=90 则x=90,作直线y=x的图象,交AB于D,∵AQ=90,∴D(90,90).
∵边界及顶点除外
∴y=x时有90﹣1=89个点符合(D点除外),(2)y=﹣x+90时,∵直线OA的解析式为y′=![]() x,∴令y=y′则x=45(
x,∴令y=y′则x=45(![]() ﹣1).
﹣1).
∵![]() ≈1.732,∴x≈32.9(取x=33),则直线OA于直线y=﹣x+90的交点是(45
≈1.732,∴x≈32.9(取x=33),则直线OA于直线y=﹣x+90的交点是(45![]() ﹣45,135﹣45
﹣45,135﹣45![]() ),再令y=0 则x=90,∵边界及顶点除外,∴y=﹣x+90时有90﹣32﹣1=57个点符合,∴有57+89﹣1=145个点符合,故选A.
),再令y=0 则x=90,∵边界及顶点除外,∴y=﹣x+90时有90﹣32﹣1=57个点符合,∴有57+89﹣1=145个点符合,故选A.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案【题目】有这样一个问题:探究函数![]() 的图象与性质.小华根据学习函数的经验,对函数
的图象与性质.小华根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)在函数![]() 中,自变量x的取值范围是________.
中,自变量x的取值范围是________.
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | m | … |
①求m的值;
②在平面直角坐标系xOy中,描出以上表中各组对应值为坐标的点,并根据描出的点,画出该函数的图象.

(2)结合函数图象写出该函数的一条性质:________.





