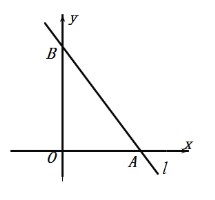题目内容
【题目】（问题）如图①，点D是∠ABC的角平分线BP上一点，连接AD，CD，若∠A与∠C互补，则线段AD与CD有什么数量关系？
（探究）
探究一：如图②，若∠A＝90°，则∠C＝180°﹣∠A＝90°，即AD⊥AB，CD⊥BC，又因为BD平分∠ABC，所以AD＝CD，理由是： ．
探究二：若∠A≠90°，请借助图①，探究AD与CD的数量关系并说明理由．
[理论]点D是∠ABC的角平分线BP上一点，连接AD，CD，若∠A与∠C互补，则线段AD与CD的数量关系是 ．
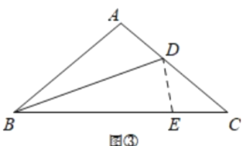
[拓展]已知：如图③，在△ABC中，AB＝AC，∠A＝100°，BD平分∠ABC．
求证：BC＝AD+BD
【答案】【探究】探究一：角平分线上的点到角的两边的距离相等；探究二： AD=CD，理由详见解析；【理论】AD＝CD；【拓展】详见解析
【解析】
探究一：根据角平分线的性质定理解答；
探究二：作DF⊥BC于F，作DE⊥AB交BA的延长线于E，证明△DAE≌△DCF，根据全等三角形的性质证明结论；
[理论]根据探究结果得到答案；
[拓展]在BC上取一点E，使BE＝BD，利用等腰三角形的性质，结合前面的结论得到DE=AD，通过证明得出CE=DE=AD即可证明结论．
解：探究一：∵BD平分∠ABC，AD⊥AB，CD⊥BC，
∴AD＝CD，
理由是：角平分线上的点到角的两边的距离相等，
故答案为：角平分线上的点到角的两边的距离相等；
探究二：AD＝CD．
理由：作DF⊥BC于F，作DE⊥AB交BA的延长线于E，
∵BD平分∠ABC，DE⊥AB，DF⊥BC，
∴DE＝DF，
∵∠BAD+∠DAE＝180°，∠BAD+∠C＝180°，
∴∠DAE＝∠C，
在△DAE和△DCF中，
，
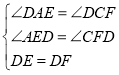∴△DAE≌△DCF（AAS）
∴AD＝CD，
故答案为：AD＝CD；
[理论]综上所述，点D是∠ABC的角平分线BP上一点，连接AD，CD，若∠A与∠C互补，则线段AD与CD的数量关系是AD＝CD，
故答案为：AD＝CD；
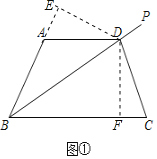
[拓展]在BC上取一点E，使BE＝BD，
∴∠BDE=∠BED，
∵在△ABC中，AB=AC，
∴∠ABC=∠C=
（180°-∠A）=40°，
∵BD平分∠ABC，
∴∠EBD=∠ABC=20°，
∴∠BDE=∠BED=（180°-∠EBD）=80°，
∴∠BED+∠A=180°，
∴由前面的结论，DE=AD，
又∵∠CDE=∠BED-∠C=40°=∠C，
∴CE=DE=AD，
∴BC=BE+EC=AD+BD，
即BC＝AD+BD．
