题目内容
【题目】已知二次函数y=ax2+bx﹣3的图象经过点(﹣1,0),(3,0).
(1)求此二次函数的解析式;
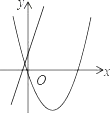
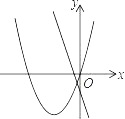
(2)在直角坐标系中描点,并画出该函数图象;
x | … | _____ | ____ | ____ | _____ | _____ | … |
y | … | _____ | ____ | ____ | ____ | _____ | … |
(3)根据图象回答:当函数值y<0时,求x的取值范围.
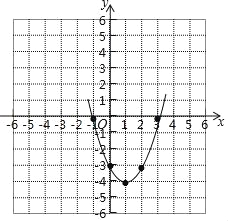
【答案】(1)y=x2﹣2x﹣3;(2)(﹣1,0),(0,﹣3),(1,﹣4),(2,﹣3),(3,0);图象见解析;(3)﹣1<x<3.
【解析】
(1)根据二次函数y=ax2+bx﹣3的图象经过点(﹣1,0),(3,0),可以求得该函数的解析式;
(2)根据(1)中的函数解析式,可以解答本题;
(3)根据(2)中所画的函数图象,可以直接写出当函数值y<0时,x的取值范围.
解:(1)∵二次函数y=ax2+bx﹣3的图象经过点(﹣1,0),(3,0),
![]() ,
,
解得,![]() ,
,
∴此二次函数的解析式为y=x2﹣2x﹣3;
(2)∵y=x2﹣2x﹣3,
∴当x=﹣1时,y=0,
当x=0时,y=﹣3,
当x=1时,y=﹣4,
当x=2时,y=﹣3,
当x=3时,y=0,
故答案为:(﹣1,0),(0,﹣3),(1,﹣4),(2,﹣3),(3,0),
函数图象如图所示;
(3)由图象可得,
当函数值y<0时,x的取值范围是﹣1<x<3.

【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?