题目内容
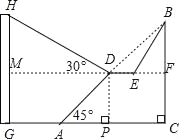
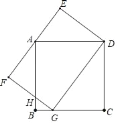
【题目】如图,点G是边长为4的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=5.
(1)寻找并证明图中的两组相似三角形;
(2)求HG、FG的长.
【答案】(1)见解析;(2) HG=![]() ,FG=
,FG=![]() .
.
【解析】
(1)根据正方形的性质和矩形的性质以及相似三角形的判定解答即可;
(2)根据相似三角形的性质解答即可.
证明:(1)∵正方形ABCD
∴∠B=∠C=90°
又∵矩形DEFG
∴∠FGD=90°
∴∠HGB+∠DGC=90°
又因为∠DGC+∠GDC=90°
∴∠GDC=∠HGB
∴△HGB∽△GDC,
相似三角形还有:△HGB∽△HAF,△DAE∽△GDC
(2)在Rt△DGC中,∵GD=5,DC=4
∴CG=3,
∵△HGB∽△GDC
∴![]()
∴HG=![]() ,
,
∵△HGB∽△ADE
∴![]()
∴DE=![]()
∵四边形DEFG是矩形,
∴FG=DE=![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
【题目】已知二次函数y=ax2+bx﹣3的图象经过点(﹣1,0),(3,0).
(1)求此二次函数的解析式;
(2)在直角坐标系中描点,并画出该函数图象;
x | … | _____ | ____ | ____ | _____ | _____ | … |
y | … | _____ | ____ | ____ | ____ | _____ | … |
(3)根据图象回答:当函数值y<0时,求x的取值范围.