题目内容
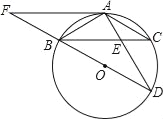
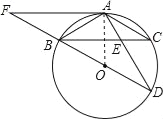
【题目】如图,△ABC为圆O的内接三角形,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.
(1)求证:△ABE∽△ADB,并求AB的长;
(2)延长DB到F,使BF=BO,连接FA,那么直线FA与⊙O相切吗?为什么?
【答案】(1)见解析,AB=2![]() ;(2)直线FA与⊙O相切,见解析.
;(2)直线FA与⊙O相切,见解析.
【解析】
(1)根据等腰三角形的性质和圆周角定理可得∠ABC=∠D,由∠BAE=∠DAB故△ABE∽△ADB,进而可得![]() ;代入数据即可得求解.
;代入数据即可得求解.
(2)连接OA,根据勾股定理可得BF=BO=AB;易得∠OAF=90°,可得直线FA与⊙O相切.
(1)证明:∵AB=AC,
∴∠ABC=∠C.
∵∠C=∠D,
∴∠ABC=∠D.
又∵∠BAE=∠DAB,
∴△ABE∽△ADB,
∴![]() ,
,
∴AB2=ADAE=(AE+ED)AE=(2+4)×2=12,
∴AB=2![]() ;
;
(2)解:直线FA与⊙O相切.
理由如下:
连接OA,
∵BD为⊙O的直径,
∴∠BAD=90°,
∴BD=![]() ,
,
∴BF=BO=![]() .
.
∵AB=2![]() ,
,
∴BF=BO=AB,
∴∠OAF=90°.
∴直线FA与⊙O相切.
故答案为:(1)见解析,AB=2![]() ;(2)直线FA与⊙O相切,见解析.
;(2)直线FA与⊙O相切,见解析.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
【题目】已知二次函数y=ax2+bx﹣3的图象经过点(﹣1,0),(3,0).
(1)求此二次函数的解析式;
(2)在直角坐标系中描点,并画出该函数图象;
x | … | _____ | ____ | ____ | _____ | _____ | … |
y | … | _____ | ____ | ____ | ____ | _____ | … |
(3)根据图象回答:当函数值y<0时,求x的取值范围.