题目内容
【题目】某兴趣小组对函数y=![]() 的图象和性质进行探究,请你帮助解决下面问题:
的图象和性质进行探究,请你帮助解决下面问题:
(1)函数y=![]() 中自变量x的取值范围是 ;
中自变量x的取值范围是 ;
(2)如表是x、y的几组对应值,则m= ;
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
(3)如图,已经画出了该函数图象的一部分,请你画出函数图象的另一部分;
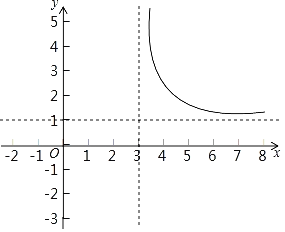
(4)该函数图象两个分支关于一个点成中心对称,这个点的坐标是 ;
(5)若函数y=![]() 的图象上有三点A(x1,y1)、B(x2,y2)、C(x3,y3)且x1<x2<3<x3,则y1、y2、y3的大小关系是 (用“<”连接).
的图象上有三点A(x1,y1)、B(x2,y2)、C(x3,y3)且x1<x2<3<x3,则y1、y2、y3的大小关系是 (用“<”连接).
【答案】(1)x≠3;(2)![]() ;(3)画出函数图象,如图所示见解析;(4)(3,1);(5)y2<y1<y3.
;(3)画出函数图象,如图所示见解析;(4)(3,1);(5)y2<y1<y3.
【解析】
(1)由分母不能为零,即可得出自变量x的取值范围;
(2)把x=-1代入函数关系式即可;
(3)描点、连线,画出函数图象即可;
(4)观察函数图象即可解答;
(5)观察函数图象即可解答.
(1)∵x在分母上,
∴自变量x的取值范围是x﹣3≠0,解得x≠3;
(2)当x=﹣1时,![]() ,
,
即![]() ;
;
(3)画出函数图象,如图所示:
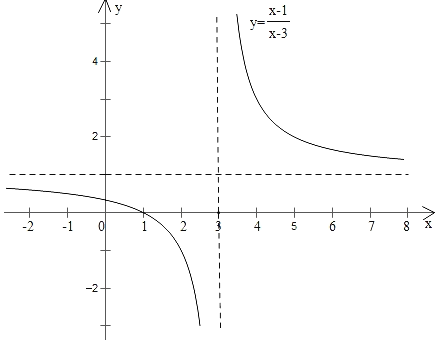
(4)该函数图象两个分支关于一个点成中心对称,这个点的坐标是(3,1);
(5)由图象可知,当x<3时,y<0且y随x的增大而减小;当x>3时,y>0,
∵x1<x2<3<x3,
∴y2<y1<y3.
故答案为:(1)x≠3;(2)![]() ;(4)(3,1);(5)y2<y1<y3.
;(4)(3,1);(5)y2<y1<y3.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】为了防范疫情,顺利复学,某市教育局决定从甲、乙两地用汽车向![]() 两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,
两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,![]() 两校分别需要口罩30万个,20万个,两地到
两校分别需要口罩30万个,20万个,两地到![]() 两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
路程 | 路程 | |
甲地 | 乙地 | |
A校 | 10 | 20 |
B校 | 15 | 15 |
(1)根据题意,在答题卡中填写下表:
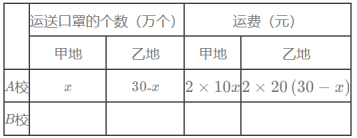
(2)设总运费为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?
的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?