题目内容
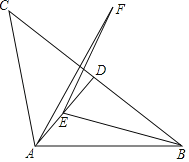
【题目】 如图,△ABC中,AB=AC,∠ABC=α,tanα=![]() ,AD⊥BC于点D,点E是线段AD上的一个动点,连接EB,将线段EB绕点E逆时针旋转2α后得到线段EF,连接AF,若BC=24,则线段AF的最小值为_____.
,AD⊥BC于点D,点E是线段AD上的一个动点,连接EB,将线段EB绕点E逆时针旋转2α后得到线段EF,连接AF,若BC=24,则线段AF的最小值为_____.
【答案】![]()
【解析】
连接BF,过点E作EH⊥BF于H,作![]() ,在BT上取一点使得AT=BT,连接AT,TE,过点T作TG⊥AB于G,证明
,在BT上取一点使得AT=BT,连接AT,TE,过点T作TG⊥AB于G,证明![]() ∽
∽![]() ,推出
,推出![]() =
=![]() =
=![]() ,得到AF=
,得到AF=![]() TE,求出TE的最小值即可解决问题.
TE,求出TE的最小值即可解决问题.
解:如图,连接BF,过点E作EH⊥BF于H,作![]() ,在BT上取一点使得AT=BT,连接AT,TE,过点T作TG⊥AB于G,
,在BT上取一点使得AT=BT,连接AT,TE,过点T作TG⊥AB于G,
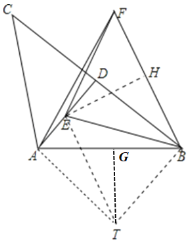
∵BE=EF,EH⊥BF,∠BEF=2α,
∴∠BEH=∠FEH=α,∠BHE=90°,BH=FH,
∴∠EBF+∠BEH=∠EBF+α=90°,
∵AB=AC,AD⊥BC,
∴∠BAD+∠ABD=90°,即∠BAD+α=90°,
∴∠EBF=∠BAD,
∵AD∥BT,
∴∠ABT=∠BAD,
∴∠ABT=∠EBF,
∴∠ABT+∠ABE=∠EBF+∠ABE,即∠TBE=∠ABF,
∵TG⊥AB于G,
∴∠ABT+∠BTG=90°,
又∵∠EBF+∠BEH=90°,
∴∠BTG=∠BEH=α,
∵tanα=![]() ,
,
∴tan∠BEH=![]() =
=![]() ,设BH=5k,EH=6k,则BF=10k,BE=
,设BH=5k,EH=6k,则BF=10k,BE=![]() k,
k,
∴![]() =
=![]() =
=![]() ,
,
∵TA=TB,TG⊥AB,
∴AG=BG,
∵tan∠ABD=![]() =
=![]() ,
,
∴设AD=5m,BD=6m,则AB=![]() m,AG=BG=
m,AG=BG=![]() m,
m,
又∵tan∠BTG=![]() =
=![]() ,
,
∴TG=![]() m,则BT=
m,则BT=![]() m,
m,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠TBE=∠ABF,
∴![]() ∽
∽![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴AF=![]() TE,
TE,
∵CD=DB=12,tan∠ABC=![]() =
=![]() ,
,
∴AD=10,AB=![]() =
=![]() =
=![]() ,
,
∴BT=AT=![]() ,
,
∵ET最小时,AF的值最小,观察图象可知当E与A重合时,ET的值最小,最小值为![]() ,
,
∴AF的最小值=![]() .
.
故答案为:![]() .
.

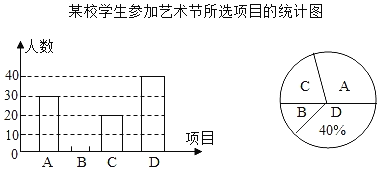
【题目】新冠疫情初期,医用口罩是紧缺物资.某市为降低因购买口罩造成人群聚集的感染风险,通过APP实名预约,以摇号抽签的方式,由市民到指定门店购买口罩.规定:已中签者在本轮摇号结束前不再参与摇号;若指定门店当日市民购买口罩的平均等待时间超过8分钟,则次日必须增派工作人员.
(1)据APP数据统计:第一天有386.5万人进行网上预约,此后每天预约新增4万人,且每天有35.5万人中签,若小明第一天没有中签,则他第二天中签的概率是多少?
(2)该市某区指定A,B两门店每天8:00-22:00时段让中签市民排队购买口罩.图1是A门店某日购买口罩的人数与等待时间的统计图,为了算出A门店某日等待9分钟的人数,小红选择14:00~16:00这个时间段到店进行统计,统计结果见表1,且这个时间段的人数占该店当天等待9分钟人数的![]() .表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
.表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
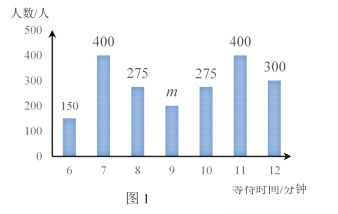
表1
时间段 | 等待9分钟/人 |
14:00~14:30 | 10 |
14:30~15:00 | 20 |
15:00~15:30 | 15 |
15:30~16:00 | 5 |
表2
等待时间 |
|
|
|
|
人数/人 |
|
|
|
|
【题目】为了防范疫情,顺利复学,某市教育局决定从甲、乙两地用汽车向![]() 两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,
两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,![]() 两校分别需要口罩30万个,20万个,两地到
两校分别需要口罩30万个,20万个,两地到![]() 两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
路程 | 路程 | |
甲地 | 乙地 | |
A校 | 10 | 20 |
B校 | 15 | 15 |
(1)根据题意,在答题卡中填写下表:
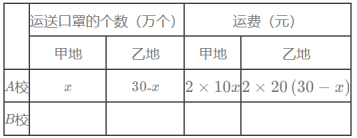
(2)设总运费为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?
的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?