Question

【题目】在平面直角坐标系中，为原点，点A（，0），点B（0，1），点E是边AB中点，把绕点A顺时针旋转，得△ADC，点O，B旋转后的对应点分别为D，C．记旋转角为．

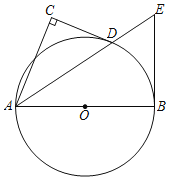
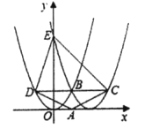
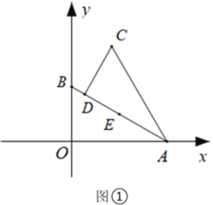
（Ⅰ）如图①，当点D恰好在AB上时，求点D的坐标；

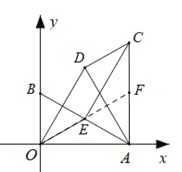
（Ⅱ）如图②，若时，求证：四边形OECD是平行四边形；

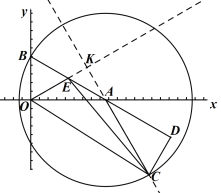
（Ⅲ）连接OC，在旋转的过程中，求△OEC面积的最大值（直接写出结果即可）．

Answer 1

【答案】（Ⅰ）D（－，）；（Ⅱ）证明见解析；（Ⅲ）．

【解析】

（1）先求出∠BAO的度数，然后求出AM、DM的长度，进而求出OM的长度，从而得出点D的坐标；

（2）先得出△BOE是等边三角形，得到OB=OE=DC，再得到OE∥DC，从而得出结论；

（3）以为圆心，为半径画，过点作交的延长线于点，当三点共线时，此时高最大，面积最大，求出的值，利用面积公式直接求解即可．

解：（Ⅰ）由题意：OA=，OB=1，

∴在△AOB中，∠AOB＝90°，tan∠BAO＝，

∴∠BAO＝30°．

由旋转性质得，DA＝OA=，

过D作DM⊥OA于M，

则在Rt△DAM中，DM=，AM=，

∴OM=AO－OM=－，

∴D（－，）．

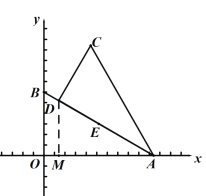
（Ⅱ）延长OE交AC于F，

在Rt△AOB 中，点E为AB的中点，∠BAO＝30°，

∴OE＝BE=AE．

又∠ABO=60°，∴△BOE是等边三角形，

∴OE=OB，∴∠BOE=60°，∴∠EOA=30°，

由旋转性质，DC=OB ，

∴OE=DC．

∵，

∴∠OAD＝60°，

由旋转性质知，

∠DAC＝∠OAB＝30°，∠DCA=∠OBA＝60°，

∴∠OAC＝∠OAD+∠DAC=90°，

∴∠OFA＝90°－∠EOA=90°－30°=60°，

∴∠DCA＝∠OFA，

∴OE∥DC．

∴四边形OECD是平行四边形．

（III）以为圆心，为半径画，过点作交的延长线于点，

在，

∵∠BAO＝30°，

∴,

∵为中点，是直角三角形，

∴，

∴，

∵圆中最长的弦是直径，

∴当点旋转到如图所示的位置时，即三点共线时，此时高最大，面积最大，

∵，

∴在中，

∵，

∴，

∴，

此时，；