题目内容
【题目】如图所示，抛物线y=ax2-
x+c经过原点O与点A（6，0）两点，过点A作AC⊥x轴，交直线y=2x-2于点C，且直线y=2x-2与x轴交于点D．
（1）求抛物线的解析式，并求出点C和点D的坐标；
（2）求点A关于直线y=2x-2的对称点A′的坐标，并判断点A′是否在抛物线上，并说明理由；
（3）点P（x，y）是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点Q，设线段PQ的长为l，求l与x的函数关系式及l的最大值．
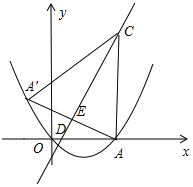
【答案】（1）抛物线解析式为y=
x2-
x．点C坐标（6，10），点D的坐标（1，0）；（2）在；（3）l=-x2+
x+
，最大值为
．
【解析】
（1）把O、A代入抛物线解析式即可求出a、c，令y=0，即可求出D坐标，根据A、C两点横坐标相等，即可求出点C坐标．
（2）过点A′作AF⊥x轴于点F，求出A′F、FO即可解决问题．
（3）设点P（x，x2-x），先求出直线A′C的解析式，再构建二次函数，利用二次函数的性质即可解决问题．
（1）把点O（0，0），A（6，0）代入y=ax2-x+c，得
，解得
，
∴抛物线解析式为y=x2-x．
当x=6时，y=2×6-2=10，
当y=0时，2x-2=0，解得x=1，
∴点C坐标（6，10），点D的坐标（1，0）；
（2）过点A′作AF⊥x轴于点F，
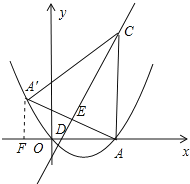
∵点D（1，0），A（6，0），可得AD=5，
在Rt△ACD中，CD=
=5
，
∵点A与点A′关于直线y=2x-2对称，
∴∠AED=90°，
∴S△ADC=
×5AE=×5×10，
解得AE=2，
∴AA′=2AE=4，DE=
，
∵∠AED=∠AFA′=90°，∠DAE=∠A′AF，
∴△ADE∽△AA′F，
∴
，
解得AF=4，A′F=8，
∴OF=8-6=2，
∴点A′坐标为（-2，4），
当x=-2时，y=×4-×（-2）=4，
∴A′在抛物线上．
（3）∵点P在抛物线上，则点P（x，x2-x），
设直线A′C的解析式为y=kx+b，
∵直线A经过A′（-2，4），C（6，10）两点，
∴
，解得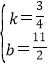
，
∴直线A′C的解析式为y=
x+，
∵点Q在直线A′C上，PQ∥AC，点Q的坐标为（x，x+），
∵PQ∥AC，又点Q在点P上方，
∴l=（x+）-（x2-x）=-x2+x+，
∴l与x的函数关系式为l=-x2+x+，（-2＜x≤6），
∵l=-x2+x+=-（x-
）2+，
∴当x=时，l的最大值为．
