题目内容
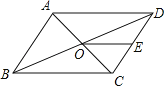
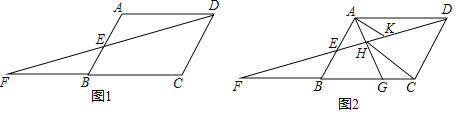
【题目】已知,如图1,在ABCD中,点E是AB中点,连接DE并延长,交CB的延长线于点F.
(1)求证:△ADE≌△BFE;
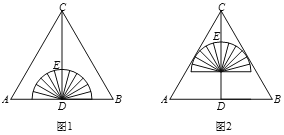
(2)如图2,点G是边BC上任意一点(点G不与点B、C重合),连接AG交DF于点H,连接HC,过点A作AK∥HC,交DF于点K.
①求证:HC=2AK;
②当点G是边BC中点时,恰有HD=nHK(n为正整数),求n的值.
【答案】(1)证明见解析;(2)证明见解析;(3)n=4.
【解析】
此题涉及的知识点是两三角形全等的判定,平行四边形的性质点的综合应用,解题时先根据已知条件证明△ADE≌△BFE,再根据两三角形相似的判定,等量代换得出边的大小关系
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠BFE,∠A=∠FBE,
在△ADE和△BFE中,
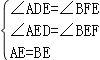 ,
,
∴△ADE≌△BFE;
(2)如图2,作BN∥HC交EF于N,
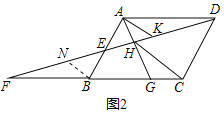
∵△ADE≌△BFE,
∴BF=AD=BC,
∴BN=![]() HC,
HC,
由(1)的方法可知,△AEK≌△BEN,
∴AK=BN,
∴HC=2AK;
(3)如图3,作GM∥DF交HC于M,
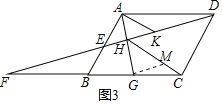
∵点G是边BC中点,
∴CG=![]() CF,
CF,
∵GM∥DF,
∴△CMG∽△CHF,
∴![]() =
=![]() =
=![]() ,
,
∵AD∥FC,
∴△AHD∽△GHF,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵AK∥HC,GM∥DF,
∴△AHK∽△HGM,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,即HD=4HK,
,即HD=4HK,
∴n=4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目