题目内容
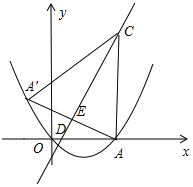
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

【答案】(1)y=![]() ;(2)最小值即为
;(2)最小值即为![]() ,P(0,
,P(0,![]() ).
).
【解析】
(1)根据反比例函数比例系数![]() 的几何意义得出
的几何意义得出![]() ,进而得到反比例函数的解析式;
,进而得到反比例函数的解析式;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,交
,交![]() 轴于点
轴于点![]() ,得到
,得到![]() 最小时,点
最小时,点![]() 的位置,根据两点间的距离公式求出最小值
的位置,根据两点间的距离公式求出最小值![]() 的长;利用待定系数法求出直线
的长;利用待定系数法求出直线![]() 的解析式,得到它与
的解析式,得到它与![]() 轴的交点,即点
轴的交点,即点![]() 的坐标.
的坐标.
(1)![]() 反比例函数
反比例函数![]() 的图象过点
的图象过点![]() ,过
,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,![]() 面积为1,
面积为1,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
故反比例函数的解析式为:![]() ;
;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,交
,交![]() 轴于点
轴于点![]() ,则
,则![]() 最小.
最小.
由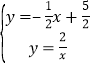 ,解得
,解得![]() ,或
,或![]() ,
,
![]() ,
,![]() ,
,
![]() ,最小值
,最小值![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
则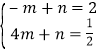 ,解得
,解得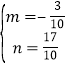 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]() 时,
时,![]() ,
,
![]() 点坐标为
点坐标为![]() .
.

练习册系列答案
相关题目