题目内容
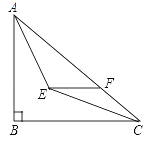
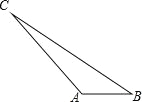
【题目】如图,在△ABC中,D、E、F分别是AB、AC、BC的中点.当△ABC满足____条件时,四边形DAEF是正方形.

【答案】AB=AC,∠A=90°.
【解析】
先根据三角形中位线定理证明四边形DAEF为平行四边形, 再补充AB=AC,可得DF=EF,从而得到平行四边形DAEF为菱形,再由一角为直角的菱形判断为正方形.
△ABC需满足AB=AC,再加上∠A=90°,可使四边形DAEF为正方形.理由如下:
证明:∵D为AB的中点,又F为BC的中点,E为AC的中点,
∴DF和EF为△ABC的中位线,
∴DF![]() AC,DF∥AC,EF
AC,DF∥AC,EF![]() AB,EF∥AB,
AB,EF∥AB,
∴四边形DAEF为平行四边形,
∵AB=AC,
∴DF=EF,
∴平行四边形DAEF为菱形,
又∵∠A=90°,
∴菱形DAEF为正方形.
故答案为:AB=AC,∠A=90°.

练习册系列答案
相关题目