题目内容
菱形ABCD中,AB=2,∠ABC=60°,顺次连接菱形ABCD各边的中点所得四边形的面积为分析:顺次连接这个菱形各边中点所得的四边形是矩形,且矩形的边长分别是菱形对角线的一半,所以可得矩形的面积.
解答:解:∵四边形ABCD是菱形,且AB=2,∠ABC=60°,
∴菱形的一条对角线长是2,另一个对角线的长是2
.
∵矩形的边长分别是菱形对角线的一半
∴矩形的边长分别是1,
,1,
.
∴矩形的面积是
.
即顺次连接菱形ABCD各边中点所得的四边形的面积为
.
故应填:
.
∴菱形的一条对角线长是2,另一个对角线的长是2
| 3 |
∵矩形的边长分别是菱形对角线的一半
∴矩形的边长分别是1,
| 3 |
| 3 |
∴矩形的面积是
| 3 |
即顺次连接菱形ABCD各边中点所得的四边形的面积为
| 3 |
故应填:
| 3 |
点评:本题考查菱形的性质,矩形的判定与性质等知识.注意准确掌握菱形的四边相等,对角线互相垂直,连接菱形各边的中点得到矩形,且矩形的边长是菱形对角线的一半.

练习册系列答案
相关题目
在菱形ABCD中,AB=5cm,对角线AC=8cm,则菱形ABCD的面积等于( )
| A、24cm2 | B、48cm2 | C、40cm2 | D、20cm2 |
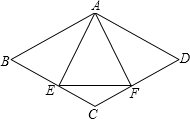 已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;
已知,如图,菱形ABCD中,E、F分别是CD、CB上的点,且CE=CF;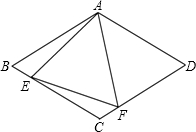 如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形边上.
如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形边上.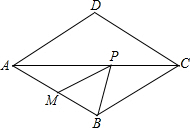 如图,菱形ABCD中,AB=5,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,则PM+PB的最小值等于
如图,菱形ABCD中,AB=5,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,则PM+PB的最小值等于 n为正整数)次这样的操作菱形中心O所经过的路径总长为
n为正整数)次这样的操作菱形中心O所经过的路径总长为