题目内容
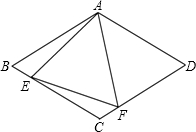 如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形边上.
如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形边上.(1)证明:不论E,F分别在边BC,CD上如何移动,总有BE=CF.
(2)在(1)的情况下,即当点E,F分别在边BC,CD上移动时,请分别探究四边形AECF和△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;
(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.
(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.
解答: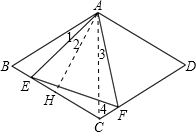 (1)证明:∵菱形ABCD,∠BAD=120°,
(1)证明:∵菱形ABCD,∠BAD=120°,
∴连接AC,
∵∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=60°
∴△ABC、△ACD为等边三角形
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
,
∴△ABE≌△ACF.(ASA)
∴BE=CF.
(2)解:四边形AECF的面积不变,△CEF的面积发生变化.
理由:由(1)得△ABE≌△ACF,
则S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF
=S△AEC+S△ABE=S△ABC,是定值,
作AH⊥BC于H点,
则BH=2,
S四边形AECF=S△ABC=
BC•AH
=
BC•
=4
由“垂线段最短”可知,
当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的面积会随着AE的变化而变化,且当AE最短时,
正三角形AEF的面积会最小,
又S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.
由(2)得,S△CEF=S四边形AECF-S△AEF
=4
-
×2
×
=
.
 (1)证明:∵菱形ABCD,∠BAD=120°,
(1)证明:∵菱形ABCD,∠BAD=120°,∴连接AC,
∵∠1+∠EAC=60°,∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=60°
∴△ABC、△ACD为等边三角形
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
|
∴△ABE≌△ACF.(ASA)
∴BE=CF.
(2)解:四边形AECF的面积不变,△CEF的面积发生变化.
理由:由(1)得△ABE≌△ACF,
则S△ABE=S△ACF,
故S四边形AECF=S△AEC+S△ACF
=S△AEC+S△ABE=S△ABC,是定值,
作AH⊥BC于H点,
则BH=2,
S四边形AECF=S△ABC=
| 1 |
| 2 |
=
| 1 |
| 2 |
| AB2-BH2 |
| 3 |
由“垂线段最短”可知,
当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的面积会随着AE的变化而变化,且当AE最短时,
正三角形AEF的面积会最小,
又S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.
由(2)得,S△CEF=S四边形AECF-S△AEF
=4
| 3 |
| 1 |
| 2 |
| 3 |
(2
|
| 3 |
点评:本题考查了菱形每一条对角线平分一组对角的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了三角形面积的计算,本题中求证△ABE≌△ACF是解题的关键.

练习册系列答案
相关题目
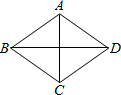 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
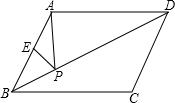
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.