Question

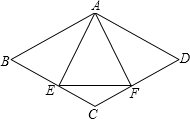已知，如图，菱形ABCD中，E、F分别是CD、CB上的点，且CE=CF；
（1）求证：△ABE≌△ADF．
（2）若菱形ABCD中，AB=4，∠C=120°，∠EAF=60°，求菱形ABCD的面积．

Answer 1

分析：（1）根据SAS即可判断出△ABE≌△ADF．
（2）连接AC，则可将菱形分成两个全等的等边三角形，从而根据AB=4可求出面积．

解答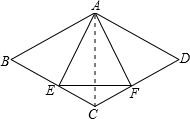：证明：（1）∵四边形ABCD是菱形，
∴AB=AD，BC=CD，∠B=∠D，
∵CE=CF，
∴BE=DF，
在△ABE与△ADF中，
∵

AB=AD ∠B=∠D BE=DF

，
∴△ABE≌△ADF（SAS）

（2）连接AC，
∵∠C=120°，
∴可得△ABC和△ACD为两个全等的等边三角形，
又∵AB=4，
S_△ABC=S_△A，DC=4

3

，
∴S_菱形ABCD=8

3

．

点评：本题考查了菱形的性质及全等三角形的判定，难度一般，解答本题的关键是根据题意条件得出证明结论需要的条件．