题目内容
已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC。
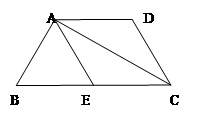
小题1:求证:四边形AECD是平行四边形
小题2:当等腰梯形ABCD满足__ ▲ 时(添加一个条件),
则四边形AECD是菱形。
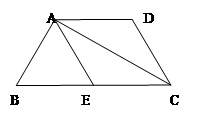
小题1:求证:四边形AECD是平行四边形
小题2:当等腰梯形ABCD满足__ ▲ 时(添加一个条件),
则四边形AECD是菱形。
小题1:∵在等腰梯形ABCD中,AD∥BC,AB=DC,
∴∠B=∠DCB,
∵AE=DC,
∴AE=AB,
∴∠B=∠AEB,
∴∠DCB=∠AEB,
∴AE∥DC,
∴四边形AECD为平行四边形;(2分)
小题2:埴加∠B=2∠DCA
∵AE∥DC,
∴∠EAC=∠DCA,
∵∠B=2∠DCA,∠B=∠DCB,
∴∠DCB=2∠DCA,
∴∠ECA=∠DCA,
∴∠EAC=∠ECA,
∴AE=CE,
∵四边形AECD为平行四边形,
∴四边形AECD为菱形.(3分)
(1)由等腰梯形的性质(等腰梯形同一底上的角相等),可得∠B=∠DCB,又由等腰三角形的性质(等边对等角)证得∠DCB=∠AEB,即可得AE∥DC,则四边形AECD为平行四边形;
(2)根据平行线的性质,易得∠EAC=∠DCA,又由已知,由等量代换即可证得∠EAC=∠ECA,根据等角对等边,即可得AE=CE,则四边形AECD为菱形.
(2)根据平行线的性质,易得∠EAC=∠DCA,又由已知,由等量代换即可证得∠EAC=∠ECA,根据等角对等边,即可得AE=CE,则四边形AECD为菱形.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 沿
沿 方向平移,使点E与点C重合,得
方向平移,使点E与点C重合,得 .
. ;
; ,当AB与BC满足什么数量关系时,四边形
,当AB与BC满足什么数量关系时,四边形 是菱形?证明你的结论.
是菱形?证明你的结论.






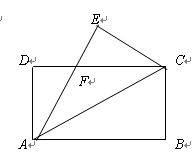
 中,
中, 两点在边
两点在边 上,且四边形
上,且四边形 是平行四边形.
是平行四边形.
 与
与 时,求证:四边形
时,求证:四边形 沿
沿 对折,若
对折,若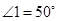 ,则
,则 等于( )
等于( )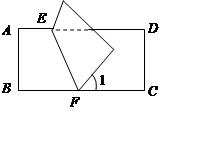




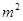 ,
,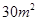 ,
,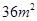 ,则种植白色花卉土地的面积为 m2.
,则种植白色花卉土地的面积为 m2.