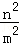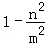题目内容
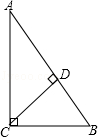
如图,在等边△ABC中,D、E、F分别是BC,AC,AB上的点,且DE⊥AC,EF⊥AB,FD⊥BC,则△DEF与△ABC的面积之比等于( )

A.1:3 B.2:3 C.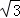 :2 D.
:2 D.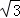 :3
:3

A.1:3 B.2:3 C.
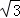 :2 D.
:2 D.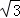 :3
:3A
试题分析:∵DE⊥AC,EF⊥AB,FD⊥BC,
∴∠C+∠EDC=90°,∠FDE+∠EDC=90°,
∴∠C=∠FDE,
同理可得:∠B=∠DFE,∠A=DEF,
∴△DEF∽△CAB,
∴△DEF与△ABC的面积之比=(
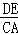 )2,
)2,又∵△ABC为正三角形,
∴∠B=∠C=∠A=60°,△EFD是等边三角形,
∴EF=DE=DF,
又∵DE⊥AC,EF⊥AB,FD⊥BC,
∴△AEF≌△CDE≌△BFD,
∴BF=AE=CD,AF=BD=EC,
在Rt△DEC中,
DE=DC×sin∠C=
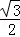 DC,EC=cos∠C×DC=
DC,EC=cos∠C×DC=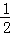 DC,
DC,又∵DC+BD=BC=AC=
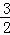 DC,
DC,∴
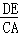 =
=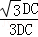 =
=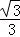 ,
,∴△DEF与△ABC的面积之比等于:(
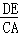 )2=
)2=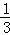 =1:3.
=1:3.故选:A.

点评:本题主要考查如何求三角形的面积之比,若能证出两个三角形是相似三角形,此时三角形的面积之比等于对应边之比的平方,只要求出对应边比即可.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目

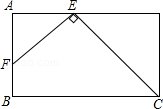
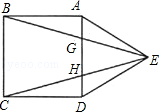
 中
中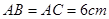 ,
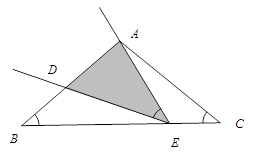
,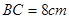 .点
.点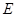 是线段
是线段 边上的一动点(不含
边上的一动点(不含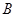 、
、 两端点),连结
两端点),连结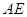 ,作
,作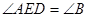 ,交线段
,交线段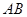 于点
于点 .
. 
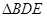 ∽
∽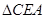 ;
; ,
,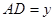 ,请写
,请写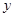 与
与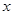 之间的函数关系式,并求
之间的函数关系式,并求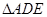 能否构成等腰三角形?若能,求出
能否构成等腰三角形?若能,求出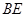 的长;若不能,请说明理由。
的长;若不能,请说明理由。
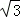 S2
S2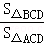 的值是( )
的值是( )