题目内容
如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
①∠AFC=∠C;
②DE=CF;
③△ADE∽△FDB;
④∠BFD=∠CAF
其中正确的结论是 .
①∠AFC=∠C;
②DE=CF;
③△ADE∽△FDB;
④∠BFD=∠CAF
其中正确的结论是 .

①③④
试题分析:在△ABC与△AEF中∵AB=AE,BC=EF,∠B=∠E
∴△AEF≌△ABC,所以AF=AC,则∠AFC=∠C;
由∠B=∠E,∠ADE=∠FDB,可知:△ADE∽△FDB;
由于∠EAF=∠BAC,所以∠EAD=∠CAF,
由△ADE∽△FDB可得∠EAD=∠BFD,
所以∠BFD=∠CAF.
综上可知:①③④正确.
点评:本题是一道基础题,但考查的知识点较多,需要根据条件仔细观察图形,认真解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


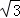 :2 D.
:2 D.
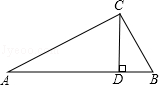

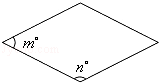
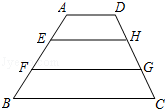
 ,设
,设 ,
, ,
, ,求A、B、C的值,并且比较它们大小.
,求A、B、C的值,并且比较它们大小.