题目内容
如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.
(1)求证:△COM∽△CBA;
(2)求线段OM的长度.
(1)求证:△COM∽△CBA;
(2)求线段OM的长度.

(1)见解析 (2)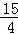
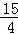
试题分析:(1)证明:∵沿直线MN对折,使A、C重合
∴A与C关于直线MN对称,
∴AC⊥MN,
∴∠COM=90°.
在矩形ABCD中,∠B=90°,
∴∠COM=∠B,
又∵∠ACB=∠ACB,
∴△COM∽△CBA;
(2)解:∵在Rt△CBA中,AB=6,BC=8,
∴AC=10,
∴OC=5,
∵△COM∽△CBA,
∴
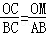 ,
,∴OM=
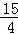 .
.点评:本题考查了相似三角形的判定与性质、勾股定理及矩形的性质,解题的关键是仔细分析并找到相等的角来证得相似三角形.

练习册系列答案
相关题目

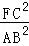 =
=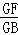 .
.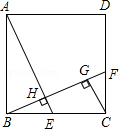
 B.
B.  C. 5 D. 6
C. 5 D. 6
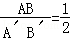 ,AB边上的中线CD=4cm,△ABC的周长为20cm,△A′B′C′的面积是64cm2,求:
,AB边上的中线CD=4cm,△ABC的周长为20cm,△A′B′C′的面积是64cm2,求:

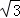 :2 D.
:2 D.