题目内容
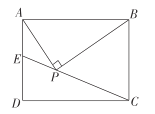
【题目】如图,在矩形ABCD中,![]() ,在矩形内有一点P,同时满足
,在矩形内有一点P,同时满足![]()
![]() ,延长CP交AD于点E,则
,延长CP交AD于点E,则![]() ______.
______.
【答案】![]()
【解析】
延长AP交CD于F,根据已知条件得到∠CPF+∠CPB=90°,根据矩形的性质得到∠DAB=∠ABC=90°,BC=AD=3,根据余角的性质得到∠EAP=∠ABP,推出AE=PE,根据勾股定理CD2+DE2=CE2即可求出AE的长,继而得到结论.
解:延长AP交CD于F,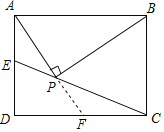
∵∠APB=90°,
∴∠FPB=90°,
∴∠CPF+∠CPB=90°,
∵四边形ABCD是矩形,
∴∠DAB=∠ABC=90°,BC=AD=3,
∴∠EAP+∠BAP=∠ABP+∠BAP=90°,
∴∠EAP=∠ABP,
∵CP=CB=3,
∴∠CPB=∠CBP,
∴∠CPF=∠ABP=∠EAP,
∵∠EPA=∠CPF,
∴∠EAP=∠APE,
∴AE=PE,
∵CD2+DE2=CE2,
∴42+(3-AE)2=(3+AE)2,
∴![]()
∴CE=3+![]() =
=![]()
故答案为:![]()

练习册系列答案
相关题目