题目内容
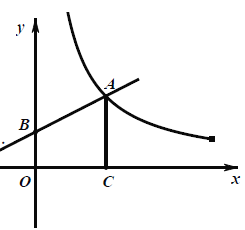
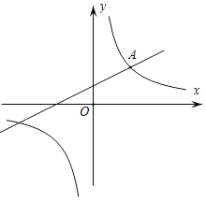
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 与一次函数
与一次函数![]() 在
在![]() 轴上方的图象的交点,过点
轴上方的图象的交点,过点![]() 作
作![]() 轴,垂足是点
轴,垂足是点![]() ,
,![]() .一次函数
.一次函数![]() 的图象与
的图象与![]() 轴的正半轴交于点
轴的正半轴交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若梯形![]() 的面积是3,求一次函数
的面积是3,求一次函数![]() 的解析式;
的解析式;
(3)结合这两个函数的完整图象:当![]() 时,写出
时,写出![]() 的取值范围.
的取值范围.
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)点A在反比例函数![]() 上,
上,![]() 轴,
轴,![]() ,求
,求![]() 坐标;
坐标;
(2)梯形面积![]() ,求出B点坐标,将点
,求出B点坐标,将点![]() 代入
代入![]() 即可;
即可;
(3)结合图象直接可求解;
解:(1)∵点![]() 在
在![]() 的图像上,
的图像上,![]() 轴,
轴,![]() .
.
∴![]() ,
,
∴![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)∵梯形![]() 的面积是3,
的面积是3,
∴![]() ,
,
解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
把点![]() 与
与![]() 代入
代入![]()
得![]()
解得:![]() ,
,![]() .
.
∴一次函数![]() 的解析式为
的解析式为![]() .
.
(3)由题意可知,作出函数![]() 和函数
和函数![]() 图像如下图所示:
图像如下图所示:
设函数![]() 和函数
和函数![]() 的另一个交点为E,
的另一个交点为E,
![]() 联立
联立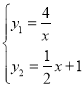 ,得
,得![]()
![]() 点E的坐标为
点E的坐标为![]()
![]()
![]() 即
即![]() 的函数图像要在
的函数图像要在![]() 的函数图像上面,
的函数图像上面,
![]() 可将图像分割成如下图所示:
可将图像分割成如下图所示:
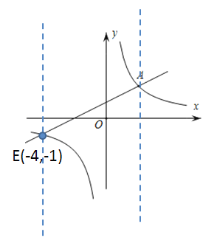
由图像可知![]() 所对应的自变量的取值范围为:
所对应的自变量的取值范围为:![]() 或
或![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
【题目】文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解10~60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |
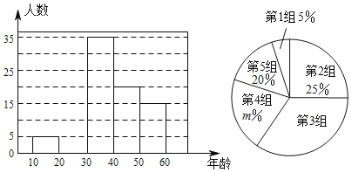
(1)请直接写出![]() ,
,![]() ,第3组人数在扇形统计图中所对应的圆心角是 度.
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有10~60岁的市民300万人,问40~50岁年龄段的关注本次大会的人数约有多少?