题目内容
【题目】在推进城乡生活垃圾分类的行动中，某校数学兴趣小组为了了解居民掌握垃圾分类知识的情况，对
两小区各600名居民进行测试，从中各随机抽取50名居民成绩进行整理得到部分信息：
（信息一）
小区50名居民成绩的频数直方图如图（每一组含前一个边界值，不含后一个边界值）；
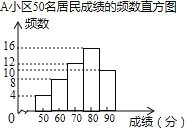
（信息二）上图中，从左往右第四组成绩如下：
75 | 77 | 77 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
（信息三）两小区各50名居民成绩的平均数、中位数、众数、优秀率（80分及以上为优秀）、方差等数据如下（部分空缺）：
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | ___________ | 79 | 40% | 277 |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息，回答下列问题：
（1）求小区50名居民成绩的中位数；
（2）请估计小区600名居民成绩能超过平均数的人数；
（3）请尽量从多个角度，选择合适的统计量分析两小区参加测试的居民掌握垃圾分类知识的情况．
【答案】（1）76；（2）300人；（3）从平均数看，两个小区居民对垃圾分类知识掌握情况的平均水平相同；从方差看，B小区居民对垃圾分类知识掌握的情况比A小区稳定；从中位数看，B小区至少有一半的居民成绩高于平均数
【解析】
（1）因为有50名居民，中位数应为第25名和第26名成绩的平均值，所以中位数落在第四组，再根据信息二中的表格数据可得出结果；
（2）先求出A小区超过平均数的人数，即（16-1）+10=25（人），再根据
小区600名居民成绩能超过平均数的人数=600×
，即可得出结果；
（3）从平均数看，两个小区居民对垃圾分类知识掌握情况的平均水平相同；从方差看，B小区居民对垃圾分类知识掌握的情况比A小区稳定；从中位数看，B小区至少有一半的居民成绩高于平均数．
解：（1）因为有50名居民，中位数应为第25名和第26名成绩的平均值.
而前三组的总人数为：4+8+12=24（人），所以中位数落在第四组，
第25名的成绩为75分，第26名的成绩为77分，所以中位数为76，
故答案为：76；
（2）根据题意得，600×
=300（人），
答：A小区600名居民成绩能超过平均数的人数300人；
（3）从平均数看，两个小区居民对垃圾分类知识掌握情况的平均水平相同；
从方差看，B小区居民对垃圾分类知识掌握的情况比A小区稳定；
从中位数看，B小区至少有一半的居民成绩高于平均数．
（答案不唯一，合理即可；）
