题目内容
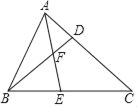
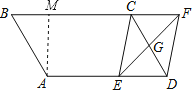
【题目】如图,平行四边形ABCD中,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.
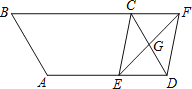
(1)求证:四边形CEDF为平行四边形;
(2)若AB=6cm,BC=10cm,∠B=60°,
①当AE= cm时,四边形CEDF是矩形;
②当AE= cm时,四边形CEDF是菱形.
【答案】(1)见解析;(2)①7;②4.
【解析】
(1)根据平行四边形的性质得出CF平行ED,再根据三角形的判定方法判定△CFG≌△EDG,从而得出FG=CG,根据平行四边形的判定定理,即可判断四边形CEDF为平行四边形.
(2)①过A作AM⊥BC于M,根据直角三角形边角关系和平行四边形的性质得出DE=BM,根据三角形全等的判定方法判断△MBA≌△EDC,从而得出∠CED=∠AMB=90°,根据矩形的判定方法,即可证明四边形CEDF是矩形.
②根据题意和等边三角形的性质可以判断出CE=DE,再根据菱形的判定方法,即可判断出四边形CEDF是菱形.
(1)证明:
∵四边形ABCD是平行四边形,
∴CF∥ED,
∴∠FCD=∠GCD,
∵G是CD的中点,
∴CG=DG,
在△FCG和△EDG中,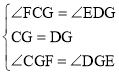
∴△CFG≌△EDG(ASA),
∴FG=EG,
∴四边形CEDF是平行四边形;
(2)①解:当AE=7时,平行四边形CEDF是矩形,
理由是:过A作AM⊥BC于M,
∵∠B=60°,AB=6,
∴BM=3,
∵四边形ABCD是平行四边形,
∴∠CDA=∠B=60°,DC=AB=6,BC=AD=10,
∵AE=7,
∴DE=3=BM,
在△MBA和△EDC中,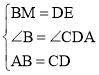 ,
,
∴△MBA≌△EDC(SAS),
∴∠CED=∠AMB=90°,
∵四边形CEDF是平行四边形,
∴四边形CEDF是矩形,
故答案为:7;
②当AE=4时,四边形CEDF是菱形,
理由是:∵AD=10,AE=4,
∴DE=6,
∵CD=6,∠CDE=60°,
∴△CDE是等边三角形,
∴CE=DE,
∵四边形CEDF是平行四边形,
∴四边形CEDF是菱形,
故答案为:4.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案