��Ŀ����
����Ŀ����ͼ����֪O��ֱ��AB��һ�㣬��BOC��90�㣬���ǰ壨MON����ֱ�Ƕ������ڵ�O���ֽ����ǰ����ŵ�O��ת��������OM��OC��ֱ��AB��ͬһ�࣮
��1������BOC��50��
����OMƽ�֡�BOCʱ�����AON�Ķ�����
����OM�ڡ�BOC�ڲ����ҡ�AON��3��COMʱ�����CON�Ķ�����
��2������COM��2��AONʱ���뻭��ʾ��ͼ�������AOM���BOC��������ϵ����˵�����ɣ�
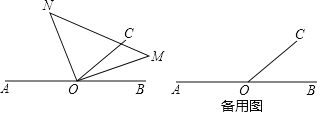
���𰸡���1����65�㣻��70�㣻��2��ͼ���������3��AOM+��BOC��360����AOM����BOC��
��������
��1��������ƽ�ǵĶ���õ���AOC��180������BOC��180����50����130�������ݽ�ƽ���ߵĶ���õ���COM��![]() ��BOC��25�������ǵõ����ۣ�
��BOC��25�������ǵõ����ۣ�
����ͼ1������COM����������AON��3���������BOM��50���������з��̼��ɵõ����ۣ�
��2������ͼ2������AON����������COM��2��������ͼ3������AON����������COM��2��������ͼ4������AON����������COM��2�������ݽǵĺͲ�ɵõ����ۣ�
�⣺��1���١ߡ�AOC��180������BOC��180����50����130����
��OMƽ����BOC��
���COM��![]() ��BOC ��25����
��BOC ��25����
�ߡ�MON��90����
���CON��90����25����65����
���AON����AOC����CON��65����
����ͼ1���ߡ�AON��3��COM��
������COM����������AON��3����
���BOM��50��������
�ߡ�MON��90����
���AON+��BOM��90����
��3��+50��������90����
�����20����
���CON��90��������70����
��2������ͼ2���ߡ�COM��2��AON��
������AON����������COM��2����
�ߡ�MON��90����
���BOM��90������AON��90��������
���BOC����BOM+��COM��90������+2����90��+����
�ߡ�BOC��90����
��������������ڣ�
����ͼ3���ߡ�COM��2��AON��
������AON����������COM��2����
�ߡ�MON��90����
���AOM��90��+������BOC��90����3����
��3��AOM+��BOC��360����
����ͼ4���ߡ�COM��2��AON��
������AON����������COM��2����
�ߡ�MON��90����
���AOM��90����������BOC��180������AOM����COM��90��������
���AOM����BOC��