题目内容
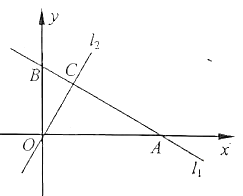
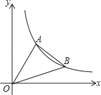
【题目】如图,直线y=![]() x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=
x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=![]() .
.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)求S△OAB.
【答案】(1) y=![]() ; (2) B的坐标为(6,2);(3)9.
; (2) B的坐标为(6,2);(3)9.
【解析】分析:(1)由点A在直线上,将x=3代入带直线解析式中求出a值,再由点A的坐标利用反比例函数图象上点的坐标特征即可得出k值,由此即可得出结论;
(2)设点B坐标为(x, ![]() ),利用正切的定义结合tanα=
),利用正切的定义结合tanα=![]() ,即可得出关于x的分式方程,解方程即可得出x的值,由此即可得出点B的坐标;
,即可得出关于x的分式方程,解方程即可得出x的值,由此即可得出点B的坐标;
(3)设直线OB为y=kx,由点B的坐标利用待定系数法即可求出直线OB的解析式,过A点做AC⊥x轴,交OB于点C,利用分割法结合三角形的面积公式即可得出结论.
详解:
(1)∵直线y=![]() x与反比例函数的图象交于点A(3,a),
x与反比例函数的图象交于点A(3,a),
∴a=![]() ×3=4,
×3=4,
∴点A的坐标为(3,4),
∴k=3×4=12,
∴反比例函数解析式y=![]() .
.
(2)∵点B在这个反比例函数图象上,设点B坐标为(x, ![]() ),
),
∵tanα=![]() ,
,
∴![]() =
=![]() ,解得:x=±6,
,解得:x=±6,
∵点B在第一象限,
∴x=6,
∴点B的坐标为(6,2).
(3)设直线OB为y=kx,(k≠0),将点B(6,2)代入得:2=6k,
解得:k=![]() ,
,
∴OB直线解析式为:y=![]() x.
x.
过A点做AC⊥x轴,交OB于点C,如图所示:
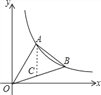
则点C坐标为(3,1),
∴AC=3.
S△OAB的面积=S△OAC的面积+S△ACB的面积=![]() ×|AC|×6=9.
×|AC|×6=9.
∴△OAB的面积为9.

练习册系列答案
相关题目