题目内容
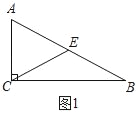
【题目】问题背景：我们学习等边三角形时得到直角三角形的一个性质：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．即：如图1，在Rt△ABC中，∠ACB=90°，∠ABC=30°，则：AC=
AB．
探究结论：小明同学对以上结论作了进一步研究．
（1）如图1，连接AB边上中线CE，由于CE=AB，易得结论：①△ACE为等边三角形；②BE与CE之间的数量关系为 ．
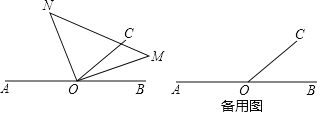
（2）如图2，点D是边CB上任意一点，连接AD，作等边△ADE，且点E在∠ACB的内部，连接BE．试探究线段BE与DE之间的数量关系，写出你的猜想并加以证明．
（3）当点D为边CB延长线上任意一点时，在（2）条件的基础上，线段BE与DE之间存在怎样的数量关系？请直接写出你的结论 ．
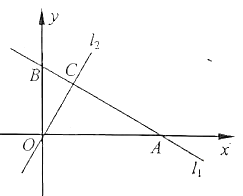
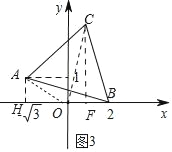
拓展应用：如图3，在平面直角坐标系xOy中，点A的坐标为（﹣
，1），点B是x轴正半轴上的一动点，以AB为边作等边△ABC，当C点在第一象限内，且B（2，0）时，求C点的坐标．
【答案】（1）EC=EB；（2）ED=EB，理由见解析；（3）ED=EB；拓展应用：C（1，2+
）．
【解析】
探究结论：（1）只要证明△ACE是等边三角形即可解决问题；
（2）如图2中，结论：ED=EB．想办法证明EP垂直平分线段AB即可解决问题；
（3）结论不变，证明方法类似；
拓展应用：利用（2）中结论，可得CO=CB，设C（1，n），根据OC=CB=AB，构建方程即可解决问题.
探究结论（1），如图1中，
∵∠ACB=90°，∠B=30°，
∴∠A=60°，
∵AC=
AB=AE=EB，
∴△ACE是等边三角形，
∴EC=AE=EB，
故答案为：EC=EB；
（2）如图2中，结论：ED=EB．
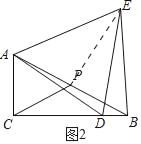
理由：连接PE，
∵△ACP，△ADE都是等边三角形，
∴AC=AD=DE，AD=AE，∠CAP=∠DAE=60°，
∴∠CAD=∠PAE，
∴△CAD≌△PAE，
∴∠ACD=∠APE=90°，
∴EP⊥AB，∵PA=PB，
∴EA=EB，∵DE=AE，
∴ED=EB；
（3）当点D为边CB延长线上任意一点时，同法可证：ED=EB，
故答案为：ED=EB；
拓展应用：如图3中，作AH⊥x轴于H，CF⊥OB于F，连接OA，
∵A（﹣，1），
∴∠AOH=30°，
由（2）可知，CO=CB，
∵CF⊥OB，
∴OF=FB=1，
∴可以假设C（1，n），
∵OC=BC=AB，
∴1+n2=1+（+2）2，
∴n=2+，
∴C（1，2+）．
