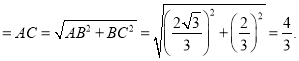��Ŀ����
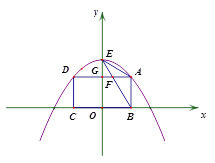
����Ŀ����ͼ1����A��D��������![]() �������㣬��B��C��x���ϣ����ı���ABCD�Ǿ��Σ���E����������y��Ľ��㣬����BE��AD�ڵ�F��AD��y��Ľ���Ϊ��G�����A�ĺ�����Ϊa(0<a<1).
�������㣬��B��C��x���ϣ����ı���ABCD�Ǿ��Σ���E����������y��Ľ��㣬����BE��AD�ڵ�F��AD��y��Ľ���Ϊ��G�����A�ĺ�����Ϊa(0<a<1).
(1) ������ABCD���ܳ�Ϊ3.5����a��ֵ��
(2) ��֤�����۵�A����˶�����EAD����ABE��
(3) ����ABE�ǵ��������Σ�
�����A�����ꣻ
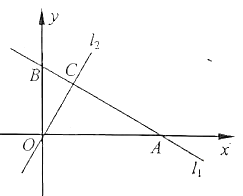
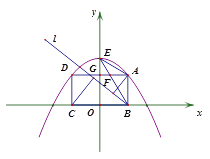
����ͼ2������ֱ��BA�Ƶ�B����ʱ�뷽����ת��ֱ��l�����A��C��ֱ��l�ľ���ֱ�Ϊ![]() ��
��![]() ����
����![]() �����ֵ.
�����ֵ.
ͼ1 ͼ2
���𰸡�(1)a=0.5��(2) �������� (3)( ![]() ��
�� ![]() )
) ![]()
�������������������1��������y���������ߵĶԳ��ᣬҲ�Ǿ���ABCD�ĶԳ��ᣬ���ݾ��ε��ܳ��г����̼��ɽ�����⣻
��2����ͼ1�У����ȹ������κ���֤��![]() ��֤��
��֤��![]() �ĵ㹲Բ�����ɽ�����⣻
�ĵ㹲Բ�����ɽ�����⣻
��3���ٹ۲�ͼ�ο�֪��![]() �ǵ���������ʱ��ֻ��
�ǵ���������ʱ��ֻ��![]() ��
��![]() ������
�У�����![]() �ɵ�
�ɵ�![]() ���
���![]() ���ɽ�����⣮
���ɽ�����⣮
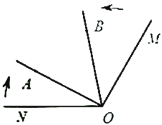
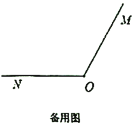
����ͼ3�У�����A��AM��ֱ��![]() ��
�� ![]() ֱ��
ֱ��![]() ��
��![]() ��
�� ![]() ֱ��
ֱ��![]() ��
��![]() ���ӳ�
���ӳ�![]() ��
��![]() ��
��![]() �����ı���
�����ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() �Ƴ�
�Ƴ�![]() ����
����![]() �����ֵ��ֻҪ��
�����ֵ��ֻҪ��![]() �����ֵ���ɣ���
�����ֵ���ɣ���![]() ���
���![]() �غ�ʱ
�غ�ʱ![]() ��ֵ���.
��ֵ���.
�����������1��������![]() ���������ߵĶԳ��ᣬҲ�Ǿ���ABCD�ĶԳ��ᣬ
���������ߵĶԳ��ᣬҲ�Ǿ���ABCD�ĶԳ��ᣬ
��![]() ����
����![]() ��Գƣ�
��Գƣ�![]()
![]()
������![]()
���![]() ��
��![]() ����ȥ����
����ȥ����![]()
��2����ͼ1�У�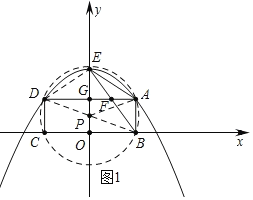
![]()
![]()
��ֱ��EB�Ľ���ʽΪ![]()
ֱ��DE�Ľ���ʽΪ![]()
![]()
![]() ��BD��OE��P��
��BD��OE��P��
��PG��AB�� ![]()
![]()
![]()
![]() �ĵ㹲Բ��
�ĵ㹲Բ��
![]()
![]() =
= ![]() ,
,![]()
��3���۲�ͼ�ο�֪��![]() �ǵ���������ʱ��ֻ��
�ǵ���������ʱ��ֻ��![]()
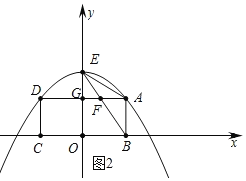
��![]() ��
�У� ![]()
![]()
���![]() ��
��![]() ����������
����������
���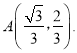
����ͼ3�У�����A��AM��ֱ��![]() ��
�� ![]() ֱ��
ֱ��![]() ��
��![]() ��
�� ![]() ֱ��
ֱ��![]() ��
��![]() ���ӳ�
���ӳ�![]() ��
��![]() ��
��![]() �����ı���
�����ı���![]() �Ǿ��Σ�
�Ǿ��Σ�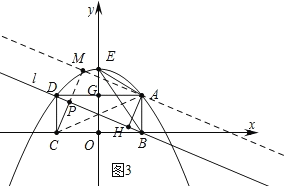
![]()
![]()
����![]()
![]() �����ֵ���ɣ�
�����ֵ���ɣ�
��![]() ��
�У� ![]()
�൱��![]() ���
���![]() �غ�ʱ
�غ�ʱ![]() ��ֵ���ʱ
��ֵ���ʱ![]()
![]() �����ֵ
�����ֵ