题目内容
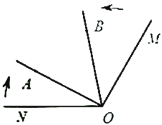
【题目】(1)如图1,在![]() 中,分别以
中,分别以![]() 、
、![]() 为斜边,向
为斜边,向![]() 的形外作等腰直角三角形,直角的顶点分别为
的形外作等腰直角三角形,直角的顶点分别为![]() ,点
,点![]() 分别为
分别为![]() 边的中点.问:
边的中点.问: ![]() 是否全等?____(填“是”或“否”);
是否全等?____(填“是”或“否”);
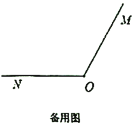
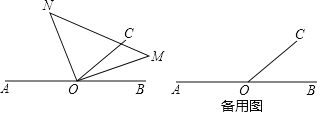
(2)如图2,在![]() 中,分别以
中,分别以![]() 为底边,向
为底边,向![]() 的形外作等腰三角形,顶角的顶点分别为
的形外作等腰三角形,顶角的顶点分别为![]() ,且
,且![]() .点
.点![]() 分别为
分别为![]()
![]() 边的中点.
边的中点.
①试判断![]() 是否满足(1)中的关系?若满足,请说明理由;若不满足,请写
是否满足(1)中的关系?若满足,请说明理由;若不满足,请写![]() 之间存在的一种关系,并加以说明.
之间存在的一种关系,并加以说明.
②若![]() ,
, ![]() ,
, ![]() 的面积为32,求
的面积为32,求![]() 的面积.
的面积.

【答案】(1)是;(2)①否, ![]() 相似,理由见解析;②
相似,理由见解析;②![]() .
.
【解析】试题分析:
(1)由已知条件易证:DF=AF=GM,FM=AG=GE,∠DFB=∠EGC=90°,∠BFM=∠BAC=∠MGC,从而可得∠DFM=∠EGM,由此即可由“SAS”证得△DFM≌△MGE;
(2)①同(1)可证得∠DFM=∠MGE,由∠BAD+∠CAE=90°,结合∠AGE=90°,可证得∠DAF=∠AEG,从而可得tan∠DAF=tan∠AEG,由此可得![]() ,结合AF=GM,AG=FM可得
,结合AF=GM,AG=FM可得![]() ,这样即可证得△DFM∽△MGE了;
,这样即可证得△DFM∽△MGE了;
②由AB=6易得AF=MG=3,结合AD=5,在Rt△ADF中易得DF=4,从而可得DF:MG=4:3,结合△DFM∽△MGE即可由△DFM的面积求得△MGE的面积了.
试题解析:
(1)是,理由如下:
∵△ABD、△AEC分别是以AB和AC为斜边的等腰直角三角形,点F、M、G分别是AB、BC、AC的中点,
∴DF=AF=GM,FM=AG=GE,∠DFB=∠EGC=90°,FM∥AC,MG∥AB,
∴∠BFM=∠BAC=∠MGC,
∴∠DFB+∠BFM=∠MGC+∠EGC,即∠DFM=∠EGM,
∴△DFM≌△MGE;
故答案为:“是”;
(2)①否, ![]() 相似;
相似;
理由:∵![]() 都是等腰三角形,且
都是等腰三角形,且![]() 为
为![]() 的中点,
的中点,
∴![]() ,∵点
,∵点![]() 分别为
分别为![]() 边的中点,
边的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
又∵![]() ,
,
∴![]() ;
;
②∵![]() ,
,
∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
∵由①知![]() ,且
,且![]() 的面积为32,
的面积为32,
∴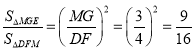 ,
,
∴![]() .
.