题目内容
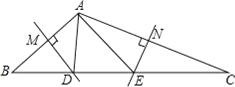
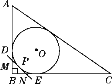
【题目】如图,已知在△ABC中,∠A=90°.

(1)请用圆规和直尺在AC上求作一点P,使得点P到BC边的距离等于PA的长;(保留作图痕迹,不写作法和证明)
(2)若AB=3,BC=5,求点P到BC边的距离.
【答案】(1)详见解析(2)1.5
【解析】
(1)作∠ABC的平分线,与AC交于点P,则点P即为所求;
(2)先由勾股定理求出AC=4,再设PA=PD=m,根据S△ABC=S△ABP+S△BCP,可得![]() ×3×4=
×3×4=![]() ×3×m+
×3×m+![]() ×5×m,求出m即可解决问题.
×5×m,求出m即可解决问题.
(1)作∠ABC的平分线BP,交AC于P,如图,
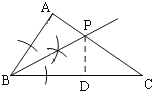
(2)在Rt△ABC中,∵∠BAC=90°,BC=5,AB=3,
∴AC=![]() =4,
=4,
设PA=PD=m,
∵S△ABC=S△ABP+S△BCP,
∴![]() ×3×4=
×3×4=![]() ×3×m+
×3×m+![]() ×5×m,
×5×m,
∴m=1.5

练习册系列答案
相关题目