题目内容
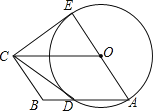
【题目】如图，四边形OABC是平行四边形，以O为圆心，OA为半径的圆交AB于D，延长AO交⊙O于E，连接CD，CE，若CE是⊙O的切线，解答下列问题：
（1）求证：CD是⊙O的切线；
（2）若BC=3，CD=4，求平行四边形OABC的面积．
【答案】（1)证明见解析；
（2）平行四边形OABC的面积S=12
【解析】
试题（1）连接OD，求出∠EOC=∠DOC，根据SAS推出△EOC≌△DOC，推出∠ODC=∠OEC=90°，根据切线的判定推出即可；
（2）根据全等三角形的性质求出CE=CD=4，根据平行四边形性质求出OA=3，根据平行四边形的面积公式求出即可．
试题解析：（1）连接OD，
∵OD=OA，
∴∠ODA=∠A，
∵四边形OABC是平行四边形，
∴OC∥AB，
∴∠EOC=∠A，∠COD=∠ODA，
∴∠EOC=∠DOC，
又∵OE=OD，OC=OC，
∴△EOC≌△DOC（SAS），
∴∠ODC=∠OEC=90°，
即OD⊥DC，
∴CD是⊙O的切线；
（2）∵△EOC≌△DOC，
∴CE=CD=4，
∵四边形OABC是平行四边形，
∴OA=BC=3，
∴平行四边形OABC的面积S=OA×CE=3×4=12．
练习册系列答案
相关题目
【题目】某工厂计划生产
两种产品共10件，其生产成本和销售价如下表所示：
产品 |
|
|
成本（万元/件） | 3 | 5 |
售价（万元/件） | 4 | 7 |
（1）若工厂计划获利14万元，则应分别生产两种产品多少件？
（2）若工厂投入资金不多于44万元，且获利不少于14万元，则工厂有哪些生产方案？
（3）在第（2）的条件下，哪种方案获利最大；最大利润是多少？
