题目内容
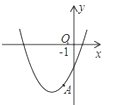
【题目】已知二次函数y=ax2+bx﹣3．
（1）若函数图象经过点（1，﹣4），（﹣1，0），求a，b的值；
（2）证明：若2a﹣b=1，则存在一条确定的直线始终与该函数图象交于两点．
【答案】(1) a=1，b=﹣2；(2)见解析.
【解析】
(1)把点（1，﹣4），（﹣1，0）代入y=ax2+bx﹣3 即可求解;(2)把b=2a代入y=ax2+bx﹣3，得出两点的坐标，验证即可.
（1）∵二次函数y=ax2+bx﹣3的图象经过点（1，﹣4），（﹣1，0），
∴代入得：
，
解得：a=1，b=﹣2；
（2）证明：∵2a﹣b=1，
∴b=2a﹣1，
∴y=ax2+bx﹣3=ax2+（2a﹣1）x﹣3=（x2+2x）a﹣x﹣3，
令x=0时，y=﹣3，
令x=﹣2时，y=﹣1，
则二次函数y=ax2+bx﹣3的图象经过定点（0，﹣3）和（﹣2，﹣1），
∴若直线过（0，﹣3）和（﹣2，﹣1），则永远与二次函数交于两点，
此直线的解析式是y=﹣x﹣3．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】某工厂计划生产
两种产品共10件，其生产成本和销售价如下表所示：
产品 |
|
|
成本（万元/件） | 3 | 5 |
售价（万元/件） | 4 | 7 |
（1）若工厂计划获利14万元，则应分别生产两种产品多少件？
（2）若工厂投入资金不多于44万元，且获利不少于14万元，则工厂有哪些生产方案？
（3）在第（2）的条件下，哪种方案获利最大；最大利润是多少？
