题目内容
【题目】如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
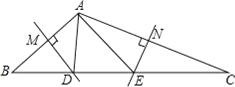
(1)若BC=10,求△ADE的周长;
(2) 设直线DM、EN交于点O
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数
【答案】(1)10;(2)点O是否在BC的垂直平分线上,理由见解析;(3)160°
【解析】
(1)由在△ABC中,AB、AC的垂直平分线分别交BC于D、E,根据线段垂直平分线的性质可得AD=BD,AE=CE,继而可得△ADE的周长=BC;
(2)①连接OB,OA,OC,证明OB=OC即可;
②根据题意得∠BOC=2∠MON,由四边形内角和可得∠BOC的度数.
(1)∵在△ABC中,AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE,
又∵BC=10,
∴△ADE周长为:AD+DE+AE=BD+DE+EC=BC=10;
(2)①如图,连接OB,OA,OC,
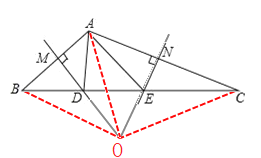
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴BO=AO,CO=AO,
∴BO=CO,
∴O在BC的垂直平分线上;
②∵OM⊥AB,ON⊥AC,
∴∠AMO=∠ANO=90°,
∵∠BAC=100°,
∴∠MOM=360°-∠AMO-∠BAC-∠ANO=80°;
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴∠BOM=∠AOM,∠CON=∠AON,
∴∠BOC=2∠MON=160°.

练习册系列答案
相关题目