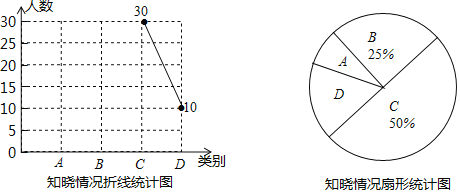
题目内容
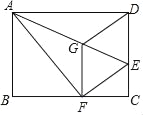
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为F.
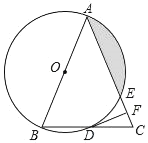
(1)求证:DF为⊙O的切线;
(2)若![]() ,∠CDF=22.5°,求阴影部分的面积.
,∠CDF=22.5°,求阴影部分的面积.
【答案】(1)见解析;(2)S阴影=4π﹣8.
【解析】
(1)连接AD、OD,则AD⊥BC,D为BC中点.OD为中位线,则OD∥AC,根据DF⊥AC可得OD⊥DF.得证;
(2)连接OE,利用(1)的结论得∠ABC=∠ACB=67.5°,易得∠BAC=45°,得出∠AOE=90°,利用扇形的面积公式和三角形的面积公式得出结论.
(1)证明:连接AD,OD.

∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴D是BC的中点,
∵O是AB的中点,
∴OD∥AC,
∴∠ODF+∠DFA=180°,
∵DF⊥AC,
∴∠DFA=90°.
∴∠ODF=90°.
∴OD⊥DF
∴DF是⊙O的切线;
(2)连接OE,
∵∠ADB=∠ADC=90°,∠DFC=∠DFA=90°,
∴∠DAC=∠CDF=5°,
∵AB=AC,D是BC中点,
∴∠BAC=2∠DAC=2×22.5°=45°,
∵OA=OE,
∴∠OEA=∠BAC=45°.
∴∠AOE=90°,
∵AE=4![]() ,
,
∴OA=OE=4.
S阴影=S扇形AOE﹣S△AOE=4π﹣8.

 小学夺冠AB卷系列答案
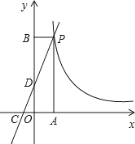
小学夺冠AB卷系列答案【题目】已知抛物线y=ax2+bx+3与y轴的交点为A,点A与点B关于抛物线的对称轴对称,二次函数y=ax2+bx+3的y与x的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 8 | 0 | 0 | … |
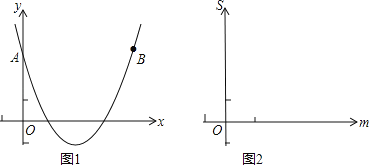
(1)抛物线的对称轴是 _________ .点A( ______, ____),B( _____, _____);
(2)求二次函数y=ax2+bx+3的解析式;
(3)已知点M(m,n)在抛物线y=ax2+bx+3上,设△BAM的面积为S,求S与m的函数关系式、画出函数图象.并利用函数图象说明S是否存在最大值,为什么?