题目内容
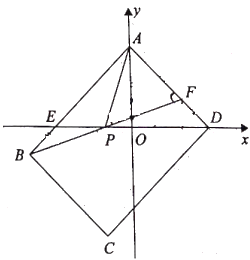
【题目】已知:如图,二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).

(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
【答案】(1)直线x=1 (2)点A′为抛物线y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 的顶点
的顶点
【解析】
试题分析:(1)把已知点O、A代入函数的解析式可求出h的值h=1,及a=![]() ,然后根据二次函数的顶点式的特点判断出对称轴;
,然后根据二次函数的顶点式的特点判断出对称轴;
(2)由线段OA绕点O逆时针旋转60°到OA′,可知OA′=OA=2,∠A′OA=60°,如图,作A′B⊥x轴于点B,根据直角三角形的特点可知sin60°=![]() ,cos60°=
,cos60°=![]() ,因此可求得A′B=OA′sin60°=
,因此可求得A′B=OA′sin60°=![]() =
=![]() ,OB=OA′cos60°=
,OB=OA′cos60°=![]() =1,所以A′点的坐标为(1,
=1,所以A′点的坐标为(1,![]() ),点A′正好是二次函数y=﹣
),点A′正好是二次函数y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 的顶点.
的顶点.
试题解析:解:(1)∵二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
∴抛物线的对称轴为直线x=1;
点A′是该函数图象的顶点.理由如下:

如图,作A′B⊥x轴于点B
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=60°,
在Rt△A′OB中,
A′B=OA′sin60°=![]() =
=![]() ,
,
∴OB=OA′cos60°=![]() =1.
=1.
∴A′点的坐标为(1,![]() ),
),
∴点A′为抛物线y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 的顶点.
的顶点.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
0<x≤200 | a |
200<x≤400 | b |
x>400 | 0.92 |
(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?